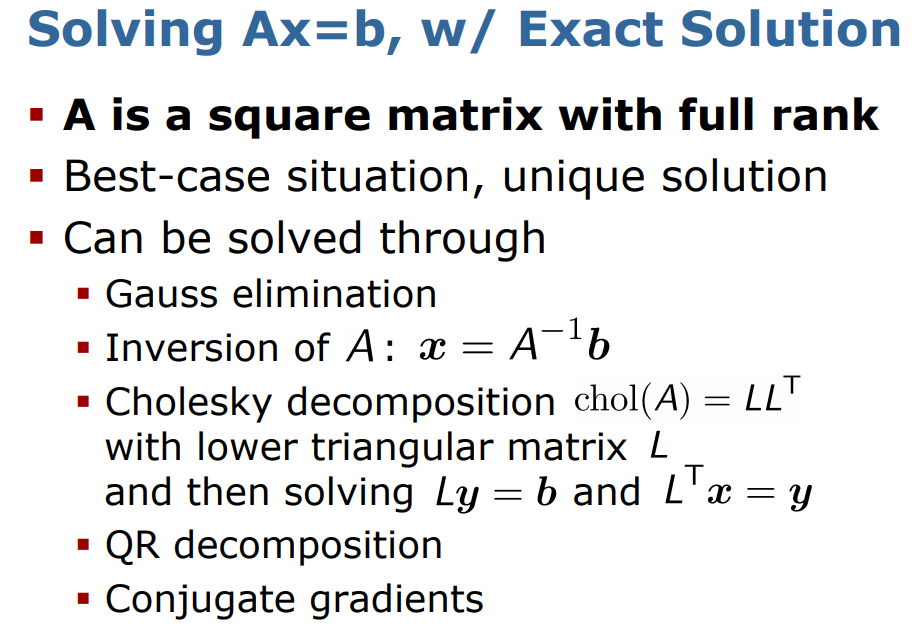본 포스팅은 https://www.youtube.com/watch?v=Q042jupFMbU&list=LL&index=23&t=2416s를 바탕으로 작성한 글입니다.

1

본 강의에선 다음 내용들에 대해 소개한다.

Ax = b 의 근 구하기

1

1

다음과 같은 세 경우로 나누어진다.

A가 정방행렬이고 A의 rank가 full rank(즉 한 열(행)벡터가 다른 벡터들로 span(선형조합으로 형성)되지 않는 경우) 일 떄, x는 다음과 같이 다양한 방식으로 구해질 수 있다 .

A가 full rank일 때

1

가우스 소거법

역행렬

숄로스키 분해(LU분해 보다 빠름. 정칙행렬 A(det(A)!=0)가 대칭행렬 (A = A^T)일 떄 사용가능, computational cost 낮음.)

등으로 구할 수 있다.

A가 over determined 일 때

1

More observations on our unknown parameter x, 즉 주어진 x의 element인 parameter보다 식(input A)이 더 많이 주어진 경우 이다.

이 경우 방정식으로 생각할 시 “해가 없음”의 경우이므로, exact한 solution x를 찾는게 아닌, Ax - b의 norm을 최소화 하는 근사값을 찾아야 한다.

x는, Ax=b 에서 양 변에 각각 A^T를 곱해주고 이후 양 변에 (A^TA)^-1 을 곱해주면 구할 수 있다.

(+정한울 교수님 머신러닝) 즉 Y = XW를(밑 슬라이드) Y = AX(위 슬라이드)로 표시한 것임 위 슬라이드에서 X -> 밑 슬라이드의 W (즉 찾아야 하는 optimal한 parameter(=weight)) 위 슬라이드에서 A -> 밑 슬라이드의 X (Input) Y = (n,1), X = (n, d), W = (d, 1) 인지하기 즉 머신러닝은 optimal한 parameter W를 찾는 것인데, 위 슬라이드에선 parameter가 다 주어진 경우이다.

1

1

머신러닝에서 optimal한 weight 찾기(정규방정식) : https://www.youtube.com/watch?v=K_EH2abOp00

https://gyeo-ri.com/29

normal equation 증명

1

A가 under determined 일 때

1

(주어진 parameter수 보다 주어진 식의 수가 적어) 해가 무수히 많기에, 만족하는 x중 x의 norm이 가장 작은 x를 찾는다.

만약 b = 0이라면, homogeneous system이 된다.

1

undetermined 환경에서, Ax = 0을 만족시키는 벡터공간을 null(A)라고 한다.

A의 dimension(=Full rank)은, (Rank(A) + Null(A))이다.