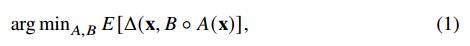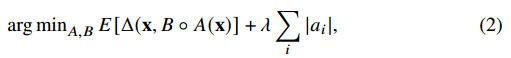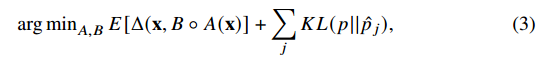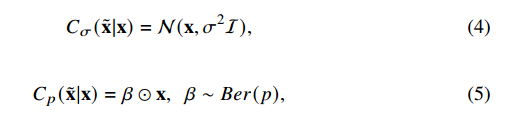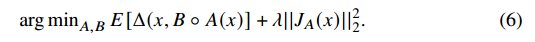원본 논문은https://arxiv.org/abs/2003.05991에 있습니다.

를 참고하여 작성한 포스트 입니다.

1. Autoencoder란

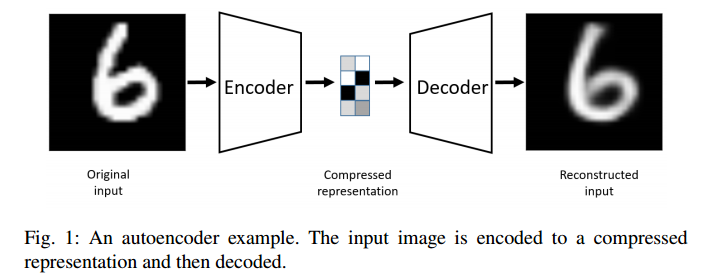
Autoencoder는 Input을 dimension을 줄인 의미있는 representation으로 encode하고, 이 representation을 decode하여 input과 같은 사이즈의 “닮은” output을 만들어 내는 네트워크이다.

만약 nonlinear한 연산이 없다면 Autoencoder의 encode 부분을 PCA로 이해할 수 있다.

Autoencoder는, end to end 방식(중간 pipeline network x)으로 한 큐에 트레이닝 될 수도 있고, 반대로 layer by layer 방식으로 트레이닝 될 수도 있다.

위 식에서

x : input image

delta : reconstrution loss function 일때,

B(A(x)) 즉 x를 인코딩 후 디코딩한 이미지가, 실제 이미지 x와 다른 차이인 loss의 기대값을 줄이는 A, B를 찾는 과정이라 할 수 있다.

참고로 reconstrution loss는 L2 norm를 사용한다고 한다.

2. Regulariuzed Autoencoders

Autoencoder에는 bias variance tradeoff가 존재한다.

Bias variance tradeoff란, 

bias : 데이터의 모든 정보 고려하지 못함(under fitting) 
(degree 1인 linear model : 데이터의 모든 정보 고려 못하므로 high bias(많이 편향됨),
새로운 데이터 들어와도 모델 크게 변형 안되므로 low variance)

variance : 데이터에 있는 노이즈까지도 학습(over fitting) 
(Polynomial with degree = 20 : 주어진 데이터 잘 고려 : low bias(편향 안됐음),

새로운 데이터 들어오면 모델 크게 변형되므로 high variance)

즉 이 두 term 간에는 tradeoff 존재

즉 너무 meaningfull한 representation 만들기 vs 너무 reconstructed 가 잘된 이미지 만들기 사이 tradeoff가 존재한다.

이 tradeoff를 줄이고자 한 autoencoders들을 소개한다.

2.1 Sparse Autoencoder

sparse(희소)한 정도에 따라 hidden layer node의 활성화 정도를 조절해주는 Autoencoder이다.

기존 Autoencoder에 ai(i번째 hidden layer)가 regularization factor로 더해진 모습이다.

위 식으로 봐도 무방한데, p hat 목표한 활성화 정도, p를 현재 활성화 정도라 생각하자.

다시 말해 각 히든 layer의 노드들의 활성화 정도를 확률 p를 갖는 베르누이 분포라 가정해 보자.

p hat을 0.1로 설정했다면, KL divergence를 minimize해야 하므로 p 역시 0.1에 가까워 져야 할 것이다.

활성화 정도를 sigm()을 거쳐 나온 output의 평균이라고 생각하면(sigmoid는 elementary wise한, 즉 각 픽셀마다 한번씩 곱해지는 연산이다),

sigmoid를 거쳐 나온 값들의 평균이 0.1에 가까우려면, sigmoid를 거치기 전 대부분의 픽셀 값은 -값을 갖고, 몇 개의 픽셀들만이 +(=유의미한)값을 가질 것이다.

참고로 sigmoid를 거친 값이 0에 가까우면 그 값은 inactive, 1에 가까우면 active한 값이라고 한다.

(2)번식의 뒤의 term을 sparsity_weight(람다) x sparsity_loss라고 이해하면,

sparsity_loss가 줄어드는 쪽으로(p가 p hat에 가까운 값을 갖도록)

hidden layer의 값들이 변할 것이고(각 layer에 매핑해주는 weight역시 변할 것)

그에 따라 일부의 hidden layer node들 만이 active할 것, 즉 영향력이 있을 것이다.

이는 cost function에서 regularization factor로 가중치 절대값을 더하는 L1 regularization에서, 일부 weight가 0으로 가는(weight decay)와 유사하다.

(weight가 아닌 각 hidden layer의 노드가 sigmoid()를 거친 값이 0에 가까움)

(참고로 L2 regularization에는 regularization factor로 w가 아닌 w^2가 있어 일부 wi노드를 0으로 죽이는게 아닌 전체적인 w의 크기는 줄이는 쪽으로 즉 덜 wiggle거리는 쪽으로 학습)

이해를 돕기 위한 코드이다. (https://excelsior-cjh.tistory.com/187)

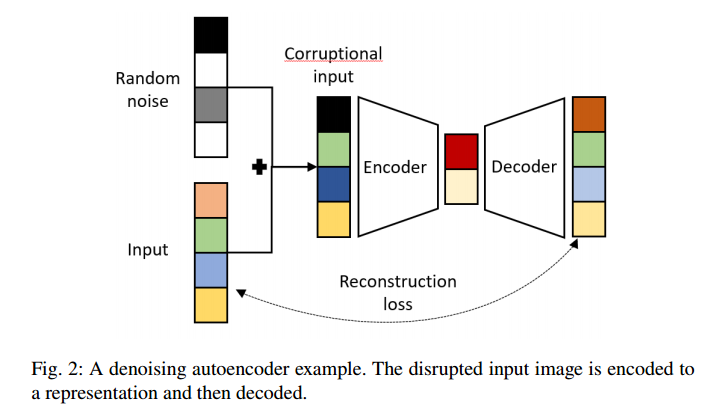
2.2 Denoising Autoencoder

Denoining Autoencoder는,

잡음에 robust(잡음 제거 용도)
regularization

두 가지 용도로 사용된다.

두 가지 denoising하는 옵션이 있는데,

첫 번째 옵션은 원본 이미지를 평균 x, 분산 시그마를 갖는 가우시안 분포(4)로 만들어준다.

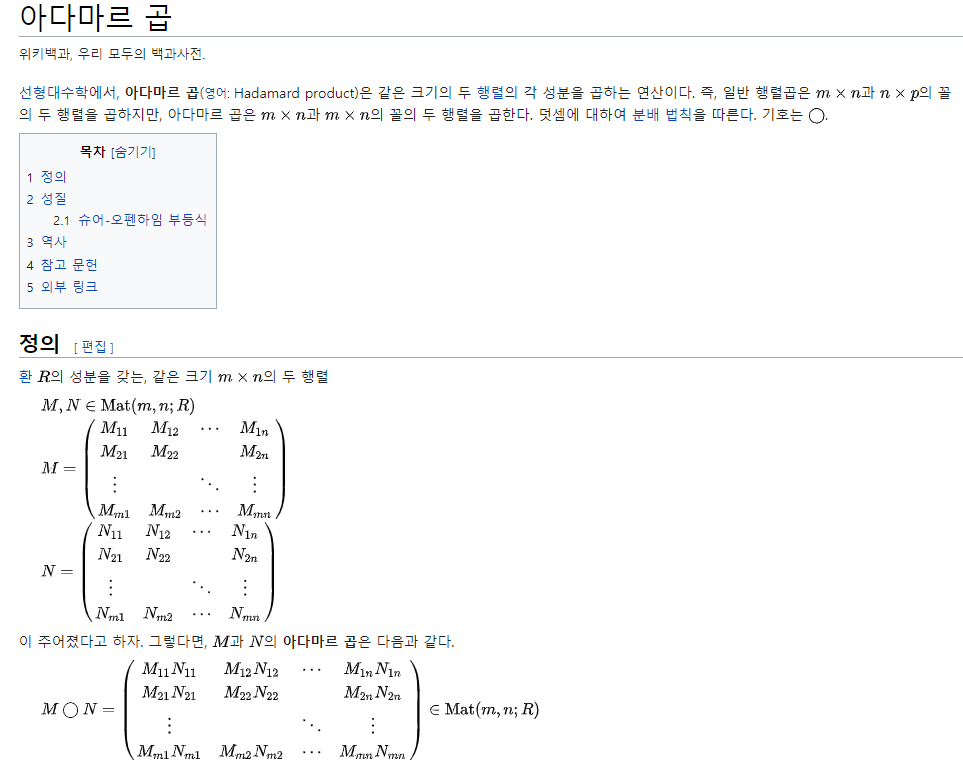
두 번째 옵션은. 원본 이미지에 베르누이 분포를 따르는 확률 베타를 x에 elementary wise product(아다마르 곱)해준다.

출처 : https://ko.wikipedia.org/wiki/%EC%95%84%EB%8B%A4%EB%A7%88%EB%A5%B4_%EA%B3%B1

두 option을 통해 reconsturcted된 이미지와, 원본 이미지(noise x)간의 loss를 줄이는 방식으로 오토인코더는 학습한다.

2.3 Contractive Autoencoder

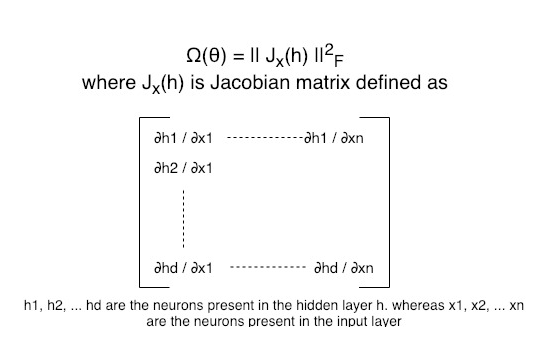
개념 - 자코비안 행렬

자코비안 행렬은, 예를 들어 (x, y, z) 좌표를 (u, v, w)좌표계로 표현할 때 필연적인 각 미소량(du, dv, dw)에 곱해지는 계수들을 모은 행렬이다.

xyz 좌표계를 원통좌표계로 바꿀 때, 앞 term으로 r이 붙는 경우를 생각하면 된다.

벡터의 미분, 전미분의 개념 : https://blog.naver.com/leesu52/90172927721

자코비안의 유도 : https://blog.naver.com/jerrypoiu/221532945268

(h1, h2, …hd) 좌표계를, (x1, x2, …xn)좌표계로 나타냈을 때 (dx1, dx2, ..dxn)앞에 곱해지는 자코비안 행렬은 다음과 같다.

Contractive Autoencoder

code : https://github.com/avijit9/Contractive_Autoencoder_in_Pytorch

Contractive autoencoder는 denoising autoencoder과 달리, input의 세세한 작은변화는 무시한다.

Encoder에게 decoder가 reconstruct할 때 중요치 않은 노이즈(변화)는 무시하며 encode하도록 한게 contractive autoencoder이다.

위 식을 보면, 앞 term인 reconstruction loss와 뒤 term인 자코비안의 L2 norm은, result를 서로 다른 방향의 값을 갖도록 유도한다.

(자코비안의 l2 norm이 커지면 reconstruction loss가 작아지는 느낌?)

자코비안의 L2 norm을 최대한 minimize하면, reconstruction이 제대로 되지 않을 것이다.

메인 아이디어는, latent representation의 variance를 줄여, 즉 reconstruction에 불필요한 variation을 regularization factor(뒤 term)를 통해 줄이고, recontruction error를 줄이는데 정말로 필요한 variation(기울기)만을 남기는게, contractive autoencoder의 main idea이다.

Contractive Auto-Encoders: Explicit Invariance During Feature Extraction (http://www.icml-2011.org/papers/455_icmlpaper.pdf)

에 자세히 나와있으니 읽어보기.

VAE(chapter 3)부터는 (2)에서 다루겠음