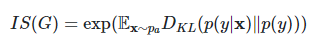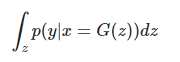IS(Inception score) and FID

https://velog.io/@tobigs-gm1/evaluationandbias

https://cyc1am3n.github.io/2020/03/01/is_fid.html

를 참고하여 작성한 포스팅 입니다.

1. 이미지의 비교

두 이미지 간 얼마나 닮았는가를 수치적으로 계산하고 싶을 때, 다음 두 distance를 이용한다.

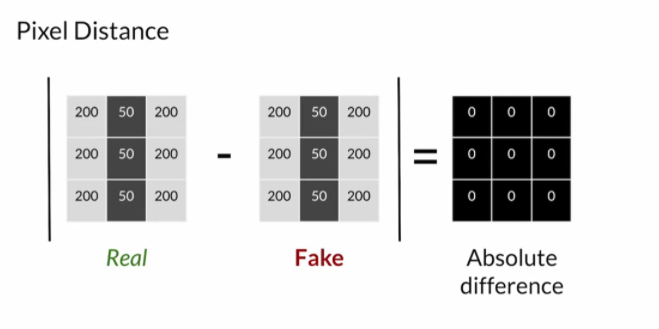
1. Pixel distance

두 이미지의 각 픽셀 간의 intensity 차이를 절대값을 통해 구한다(pixel distance). Rotation, scale 변화 등 위상변화에 취약하다.

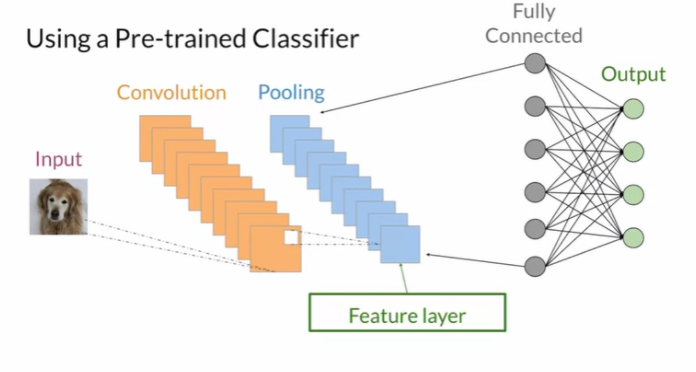
1. Feature distance

Imagenet dataset으로 학습된 weight를 이용하여 pretrained CNN(inception-v3 모델 사용)을 통해 feature distance를 구한다.

통상적으로 VGG를 예를 들 경우 Conv layer 중간 단 ~ FC 전 단 까지의 conv layer가 feature를 가장 잘 뽑아내므로 이 중 한 단의 layers를 통해 feature를 extraction 한다.

예를 들어 그 layer 단이 (512, 16, 16)이라면 채널 수 512에 해당하는 512개의 feature map에 각 그 이미지의 512개의 feature 에 해당하는 값들이 각각 담긴다. (첫 feature map : 눈에 대한 feature map, 두 번째 feature map : 코에 대한 feature map 등)

수식으로 표현하면 다음과 같다.

ϕ: Embedding function, x: input image ϕ(x)=(x1, x2,…,xn)^T , xi: 어떠한 특징의 값

이렇게 얻어진 벡터 ϕ(x)를 통해 Euclidian(or Cosine) distance를 이용해 feature distance를 구한다.

2 FID(Fréchet Inception Distance)

Embedding vector(각 feature를 나타내는 수치를 포함한 벡터)는 예를들어 512 채널일 경우 512개가 생길 것이다.

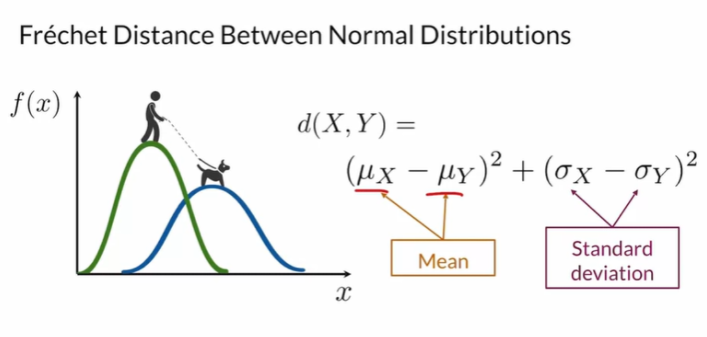
Embeding vector가 다변량 정규분포를 가진다고 가정할 때(mu, sigma를 잘 다루기 위해 가정) FID는 다음과 같다.

첫 term인 mux - muy는, 두 이미지 X, Y의 feature간의 평균 값간의 거리를 구한 것이다. 두 feature간 평균 값의 거리가 적으면 FID가 낮을 것이다.

두번째 term인 Trace() term은, X와 Y 각각 공분산 행렬을 구한후 연산한 파트이다.

Σx = (1/n)(X^T)X ..(n은 channel(feature 수)), 예를 들어 X가 (batch_size, channels) = (10, 512)이면 Σx는 shape가 (512, 512)인 공분산 행렬이 된다.

공분산 행렬을 통해 각 특징 쌍(각 row라 생각)이 얼마나 닮았는지도 알 수 있고, 대각성분들을 통해 그 feature에 해당하는 크기가 얼마인지도 알 수 있다.

만약 Σx 와 Σy가 pixelwise하게 수치 차이가 미미하다면, Trace term은 매우 작을 것이고 FID는 낮을 것이다.

따라서 두 term을 종합하여 판단할 때, 두 이미지의 feature extraction한 값이 비슷하면 FID 수치가 작을 것이고, 실제로 육안으로 보았을 때 두 이미지는 비슷할 것이다.

2-1 FID - code

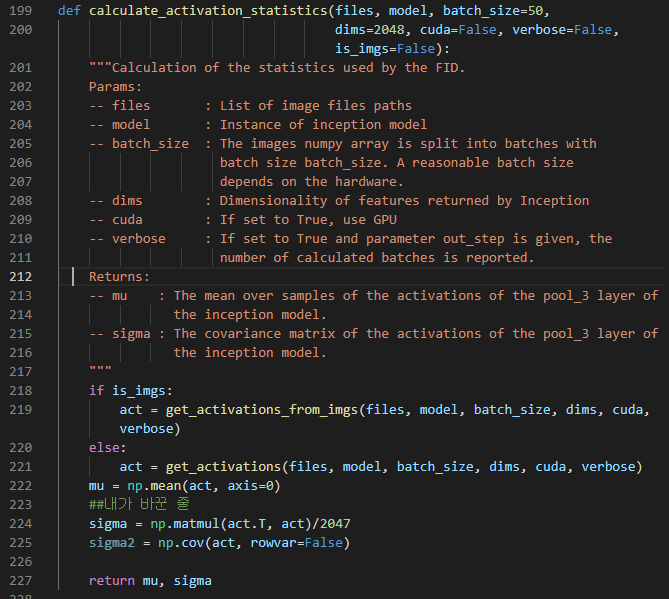
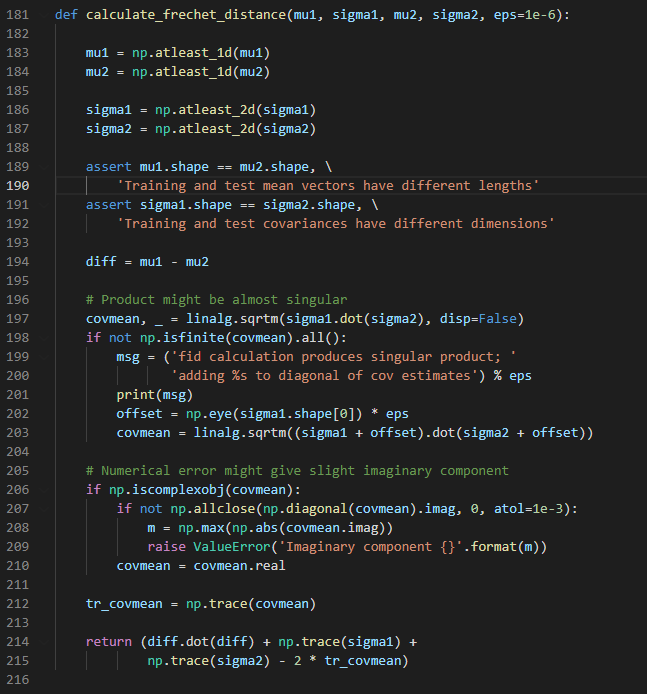
mu, sigma 구하기

FID 연산

2-2 FID - Implementation

실제로 FID를 구해보았다.

내가 StyleGAN - ADA로 생성한 이미지에 가우시안 노이즈를 iteration을 돌며 추가하여 augment한 5장의 이미지와,

StyleGAN을 학습시킬 때 사용한 400장의 웹툰 이미지간 FID를 구해보았다.

본 FID를 구한 절차에는 오류(?)가 두 가지 있다.

1. Inception v3모델이 Imagenet dataset의 weight로 학습되었기에, 웹툰 도메인의 feature extraction에는 적절치 않다는 점

2. 두 dataset의 size가 너무 적다는 점 (5장, 400장 간의 feature distance를 비교하기엔 sample size가 너무 작다.) -> (random seed를 통한 생성 이미지 augmentation, 400장을 dataloader를 통한 augmentation) 하여 비교했으면 더 나았을 수도 있을 것 같다.

그래도, 해보았다.

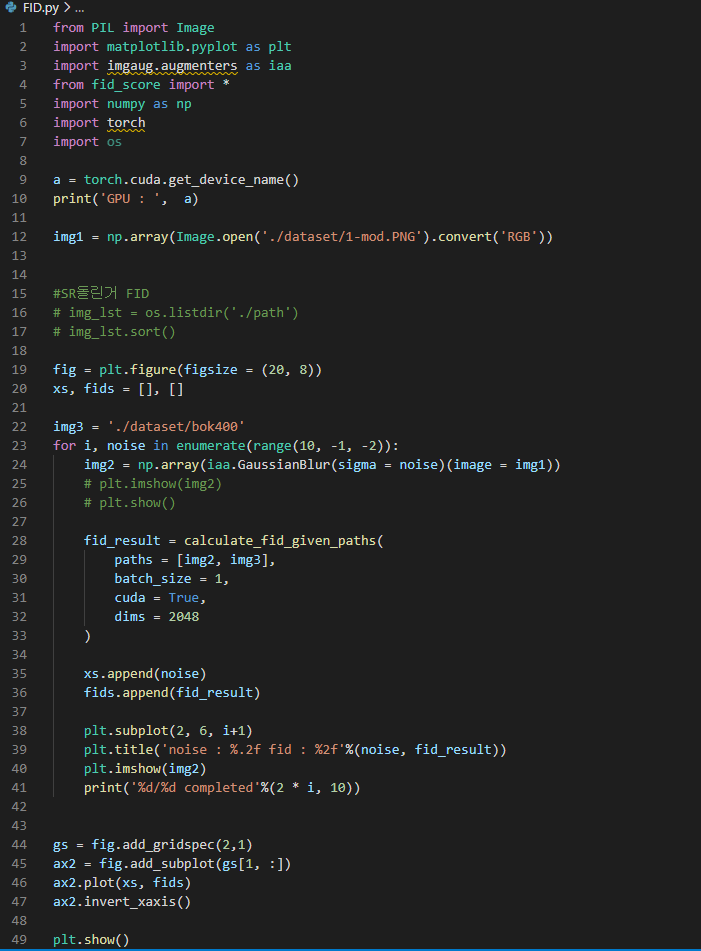
코드는 다음과 같다.

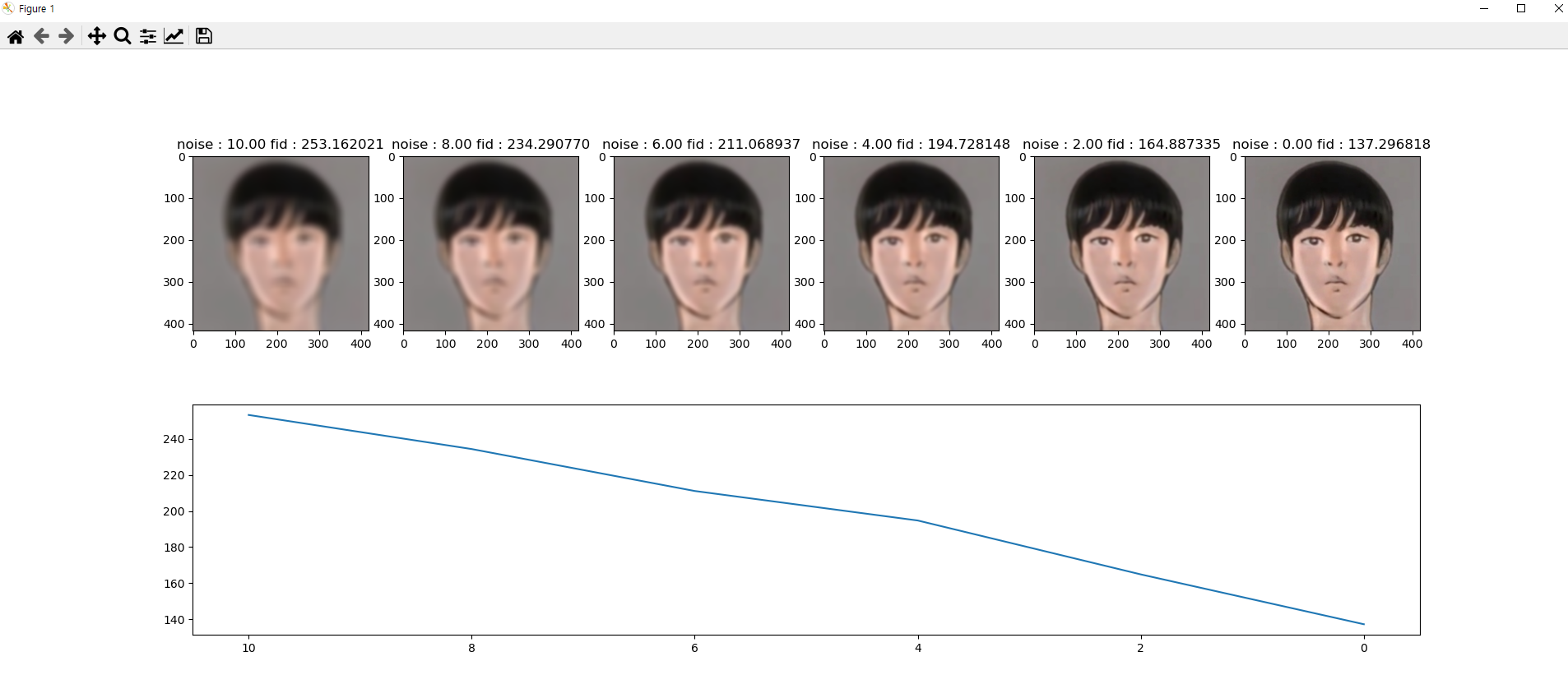
결과

noise가 제거될수록 FID가 낮아지는 모습을 볼 수 있다.

3. IS(Inception Score)

https://cyc1am3n.github.io/2020/03/01/is_fid.html를 참고하여 만들었습니다.

IS는 FID 이전 GAN을 평가할 때 주로 쓰인 metric이며, IS 이전에는 사람의 주관적 평가에 의존했다고 한다.

IS의 수식은 다음과 같고 이에 대해 설명하겠다.

IS는 생성된 이미지의 품질을 평가할 때 다음 두 가지를 고려한다.

1. Fidelity

2. Diversity

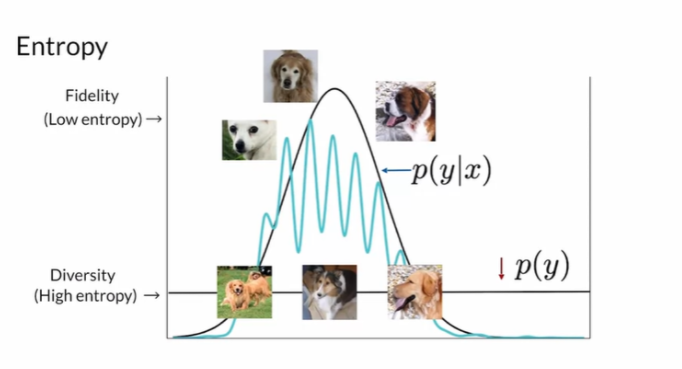
   Fidelity는, P(yㅣx)에 해당한다.

   x는 생성된 이미지, y는 label이다.

   GAN에서는 P(yㅣx)가 높기를, 즉 생성된 이미지를 보고 class(label)를 예측하기 쉬워야 한다.

   엔트로피 측면에서 보면, 엔트로피가 낮은(uniform distribution이 아닌 쏠림형) 일 것이다.

   Diversity는, P(y)에 해당한다.

   P(y)는 주변 확률 분포를 통해 계산이 가능 하다.

만약 x가 생성한 모든 y의 분포를 보았을 때 uniform하다면 entrophy가 높을 것이다.

이를 그림으로 표현하면 다음과 같다.

KL divergence는 두 분포 (p(yㅣx), p(y))가 닮은 분포이면 낮은 값, 다르면 높은 값이 나온다.

Fidelity는 쏠림형, Diversity는 unifrom형으로 분포가 나오는 것이 최적의 경우이므로 만약 생성된 이미지가 결과가 좋으면 KL divergence의 기대값이 높을 것이고, IS 역시 높을 것이다.

3-1 IS의 특징

• IS는 FID와 달리 Fully connected layer를 사용한다. (class predict를 해야 하므로)

• 생성된 이미지 만을 평가한다(real 이미지와 비교 불가능)

• FID와 마찬가지로 ImageNet data로 pre-trained된 경우 ImageNet data 이미지의 class와 다른 이미지를 다룰 경우 원하는 특징을 extract 불가능

• Generator가 각 label마다 하나의 이미지만 반복해서 생성하는 경우 IS가 높지만 이는 inner diversity를 고려하지 못한 좋지 못한 생성 모델