KL, JSD and Wasserstein distance
by
본 포스팅은 여기, 여기 여기 를 참고하여 작성하였습니다.
KL divergence
어떤 분포 p가, 다른 분포 q에 대해 얼마나 떨어져 있는지를 알려준다.
p가 q에 대한 정보량을 얼마나 잘 표현하는가? 를 나타내주는 지표이다.
정보이론에서 정보량이라 함은
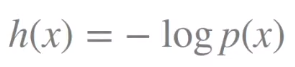
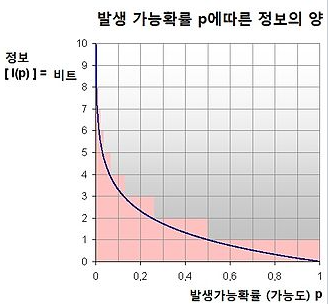
다음과 같은 식으로 나아내어진다.
p값이 0.1 근처인, 즉 잘 일어날 것 같지 않은 일이 일어나면 정보량(놀람의 정도)가 커진다.
반대로 p값이 1 근처인, 당연히 일어날 것 같았던 일이 일어나면 정보량은 0에 가깝다.
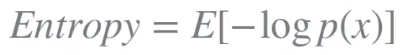
이 정보량에 대한 평균(기대값)을, 엔트로피라 하고 이 엔트로피는 불확실성이 얼마나 큰지에 대해 나타내어주는 지표이다.
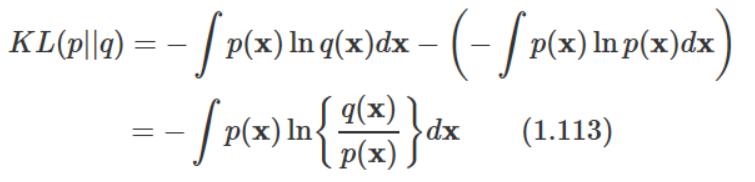
위 식은 KL divergence에 대한 식이다.
확률 분포 p와 q의 분포가 얼마나 다른지를 나타내 준다.
식을 살펴보면 p에 대한 q의 정보 손실량임이 나타난다.
p와 q 가 같을 시 최소값인 0을 갖게 된다.
알파벳이 5개 쓰인 카드를 뽑을 때,
원래 분포와 uniform 분포, 이항 분포를 비교했을 떄의 KL divergence는 다음과 같다.

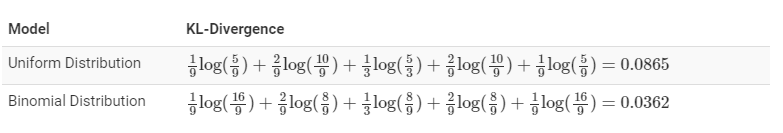
이항 분포의 경우가 kl divergence 값이 적음을 볼 수 있다.
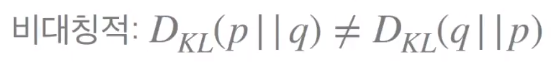
KL divergence의 단점으로는, 첫 번째로 비대칭적이다.
p에서 q에 대해 kl divergence 한 값과, q에서 p에 대해 KL divergence를 구한 값이 다르다.
두 번째로, p가 0애 가까운 값으로 간다면, q의 효과는 점점 무시된다.
따라서 분포 사이의 유사도 측정이 어려워진다.
JS divergence
JS divergence는, KL divergence의 기존 단점을 보완했다.
특징으로는 [0 ~ 1] 사이의 값을 가지고, KL divergence와 달리 대칭적이다.
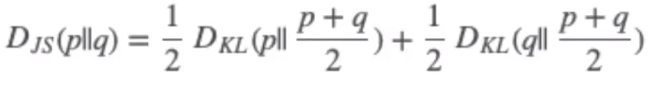
따라서 KL divergence보다 smooth 하다고 볼 수 있다.
p와 p, q의 평균에 대한 KL divergence, q와 p, q의 평균에 대한 KL divergence를 평균냄을 통하여 구할 수 있다.
GAN에서, loss 함수를 최적화 하는것은 JS divergence를 최적화 하는 것과 같다.
GAN이 KL 대신 JS 발산을 써서 더욱 성능이 잘 나왔다는 의견이 있다고도 한다.
자세한 내용 : [https://www.youtube.com/watch?v=FGP20ciUxlo&list=PLARB0SINpZ866obduFbK3xowd0JQy3PNw&index=27]
Wasserstein distance
(p)Wasserstein distance는, 다음과 같이 뮤와, 누 사이의 거리로 나타난다.
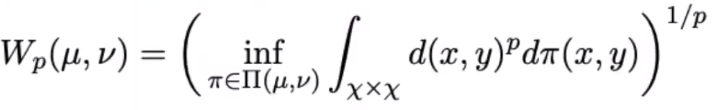
p에 1을 집어 넣으면,

식은 다음과 같아지고 이를 1 Wasserstein distance라 한다.
[https://jonathan-hui.medium.com/gan-wasserstein-gan-wgan-gp-6a1a2aa1b490] 보기
질량과 거리의 개념
EMD : 확률 분포를 다른 확률 분포로 바꾸기 위해 얼마나 많은 질량을, 얼마의 거리만큼 옮겨야 하는가? 에 대한 수치.
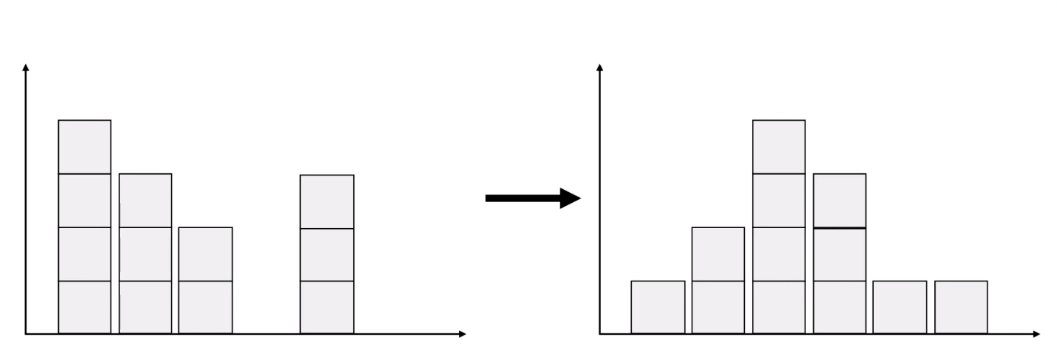
왼 쪽에서 오른쪽으로 옮기는 방법은 매우 많을테지만, 질량과 거리가 혼합된 ‘비용’을 최소화 하는 것이 목적이다.
질량과 거리만큼 이동하여 드는 힘의 총량이 Wasserstein 1 거리라고 할 수 있다.
Π(pr, pg)는 pr, pg 사이에서 가능한 모든 결합 분포이고,
γ(x, y)는 Π공간에서 존재하는 분포중 하나를 샘플링 해온 것이다.
따라서 저 박스 친 부분은, 확률 분포 p 에서 q로 이동하는 데 들어가는 에너지의 총량이라 할 수 있다.(질량 * 거리 의 총량)
정리하면 이 식은 inf(greatest lower bound, 최대 하한), 다시 말해 Π(pr, pg)(pr, pg 사이에서 가능한 모든 결합 분포) 에서 샘플링해온 γ를 통해 구한 기대값의 하한 이다.
즉 EMD에서 가장 비용이 작은 값을 Wasserstein distance라 한다.
Wasserstein distance을 KL, JSD 대신 쓰는 이유
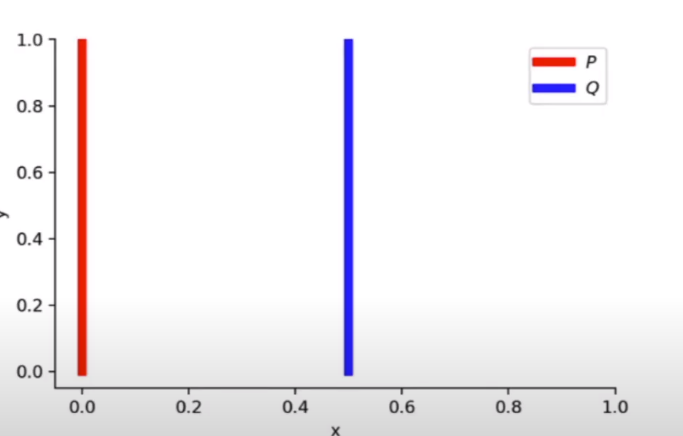
P, Q에 대해, 아예 겹치는 부분이 없다면 divergence의 계산이 어렵다.
P의 경우 x값은 0, Y는 0~1사이 균등한 값을 갖는다.
Q의 경우 x값은 임의의 세타 값(예 : 0.5), Y는 0~1사이 균등한 값을 갖는다.
이 때 KL divergence를 구하면 다음과 같은 허무맹랑한 값이 나온다.
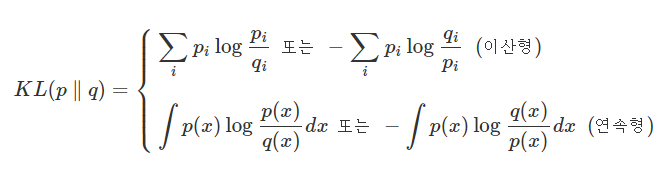
(에 대입)
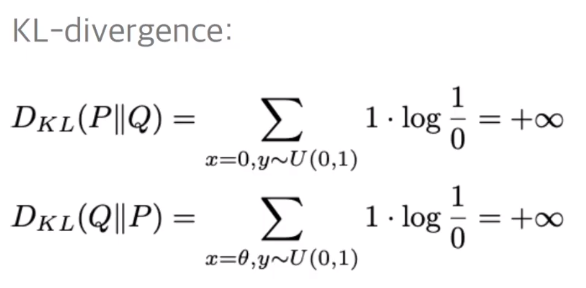
JSD 역시, 값이 나오긴 하지만 상수 값이 나오므로 gradient descent를 하는 데에는 아무 도움이 되지 않는다,
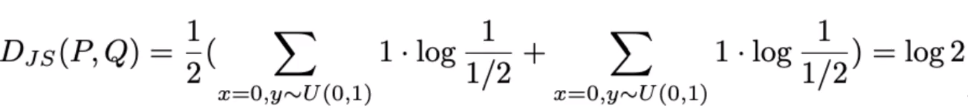
반면에 JSD는, 거리 개념인 절대값 세타를 갖기에, (x-y) , gradient descenting이 좀 더 잘되고, 안정적으로 학습이 된다고 한다.
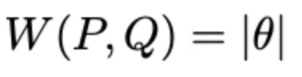
Subscribe via RSS
