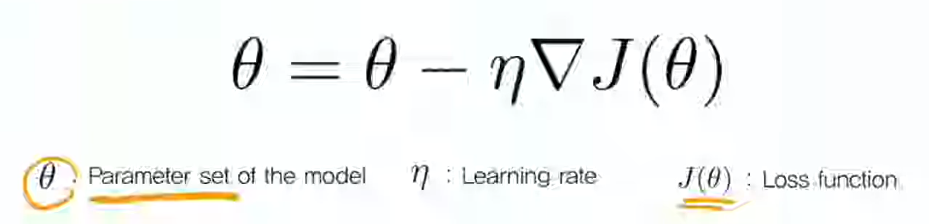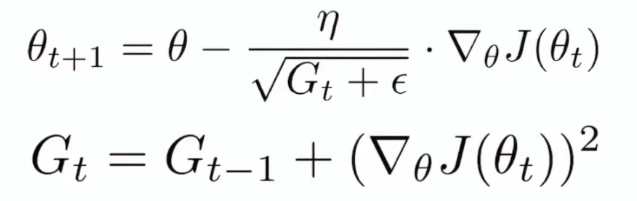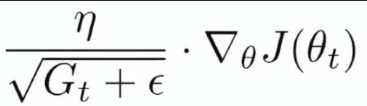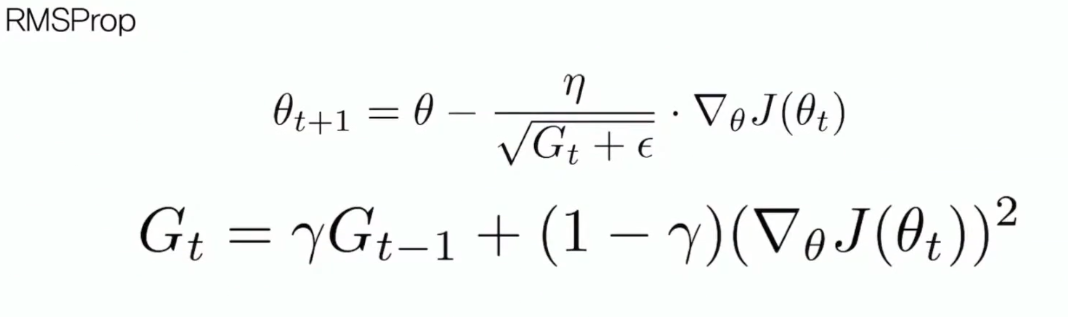딥러닝에 사용되는 Optimizers
by
본 포스트 여기를 바탕으로 작성하였습니다.
Optimizers
옵티마이저란, 머신러닝 학습 프로세스에서 실제로 파라미터를 갱신시키는 부분을 의미한다.
학습 속도를 빠르고 안정적이게 하는 것이라 말할 수 있다.
Gradient Descent
Gradient descent, 파라미터 세타에 대해, loss에 대한 gradient를 계산하고, 그 gradient 만큼 스텝을 밟아 나간다.
수식을 보면, 파라미터 세트 세타에 대해, loss function의 세타에 대한 gradient를 계산 후, learning rate를 곱하여 빼주는 방식이다.
이를 iterative 하게 반복하여, mininum을 찾아간다.
Gradient descent는, stochastic, batch 두 방식으로 방법이 나누어진다.
Batch gradient descent 방식은 매 step 갱신 시, 가지고 있는 전체 training dataset에 대해 gradient를 계산 후 업데이트 한다.
한 스텝을 밟는데 시간, 메모리 측면에서 비효율적이다.
Stochastic gradient descent(SGD)는, batch 방식과 달리 training data 전체에 대해 gradient를 계산하는 것이 아니라 매 스텝마다 작은 chunk, 즉 작은 덩어리(mini batch)만에 대해서만 gradient를 계산하고 step을 밟는다.
Mini batch를 통해 스텝을 돌리므로 시간, 메모리 면에서 우위가 있다.
GPU 메모리에 이미지를 올리는 것을 생각할 떄, 이미지의 경우 학습시켜야 할 파라미터가 많아지기에 전체 training dataset을 한 번에 메모리에 올리지 못한다.
따라서 배치를 chunk를 나누어 한 chunk를 병렬적으로 계산하고, 또 chunk를 불러와 계산하고.. 하는 방식인데, mini batch를 사용한다면 배치를 chunk로 몇 번 안나누어도 되고 이 면에서 시간적 이득을 얻는다.
Stochastic 은 deterministic과 반대되는 개념이고, deterministic이란 어떤 한 계산에 대해 유일하게 하나의 값 만을 갖는 다는 뜻 이다.
반대로 Stochastic 방식은 한 계산에 대한 결과값이 하나만 나오는게 아니라 결과의 후보가 여러가지 나오고 그에 대한 확률까지 나오는 방식이다.
SGD의 경우 미니 배치를 어떻게 고르느냐에 따라 결과 값이 다르므로, “결과가 확률적이다.” 라는 성질 때문에 stochastic 방식이라 말 할 수 있다.
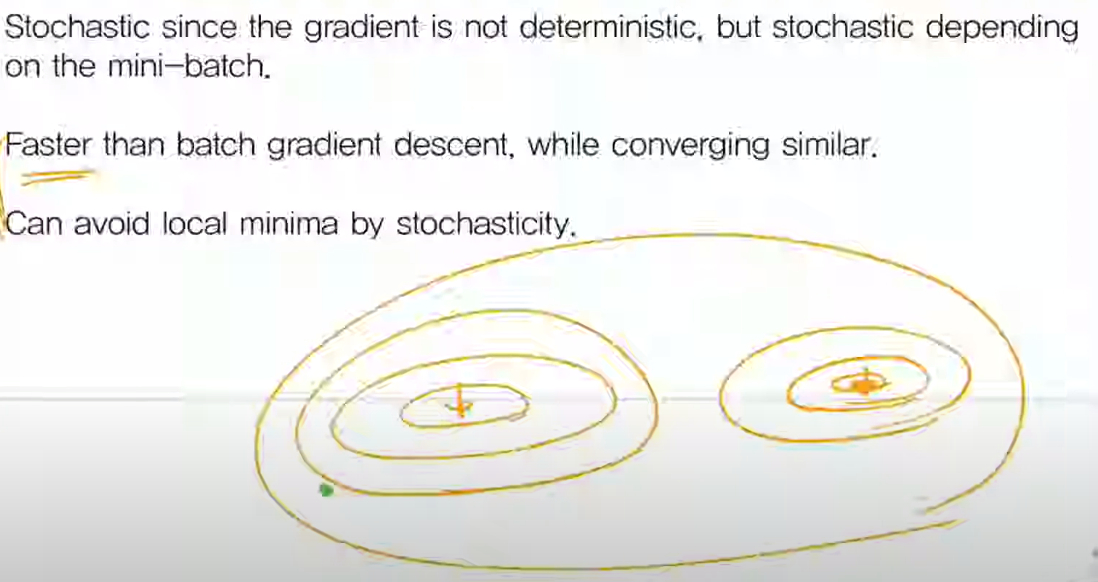
SGD의 또다른 장점은 local minimum을 피할 수 있다는 점이다.
파라미터가 두 개이고 왼쪽이 local, 오른쪽 등고선 점이 global minimunm인 그림이다.
Batch 방식의 경우 초록점에서 시작시 local minimun 쪽으로 직행 하게 된다.
SGD의 경우, 전체 training set을 이용해 loss를 구하는 것이 아니므로, minimum을 찾아가는 방향이 batch처럼 왼 쪽 local minimum으로 가는게 아니라, 다른 방향을 가질 수도 있다.
이를 통해 local minimum을 피할 수 있긴 하지만, 아닌 경우도 많고 그 점을 보완한 것이 advanced gradeint descent 알고리즘이다..
Advanced Gradient Descent
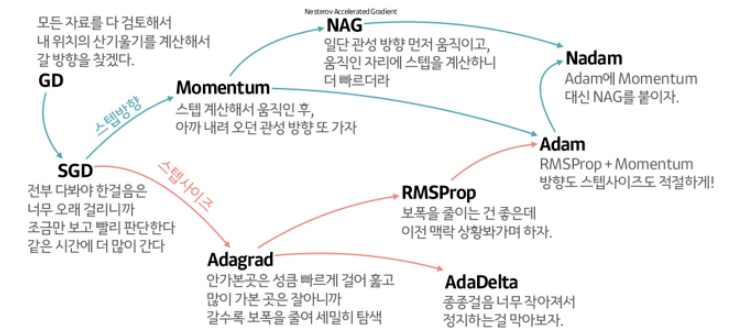
SGD에서 진화시켜, momentum 개념을 더한 것이 위쪽 branch이고, 각 parameter에 대해 다른 learning rate를 적용시키면 어떨까? 의 개념을 더한 것이 아래쪽 branch이다.
그리고 이 두 장점을 합친것이 Adam optimizer 이다.
기존 vanilla SGD의 문제점은, local minimum에 대한 취약점이다.
Momentum
Momentum 개념을 이용하면, local minimum과 oscillating 문제에 대해 어느정도 대응이 가능해 진다.
먼저 local minimun의 경우, U자 계곡에서 공을 굴리면 공이 바로 minimum에서 멈추는 것이 아니라 관성에 의해 반대쪽 벽도 어느정도 오른 후 이 과정을 반복하며 멈춘다.
기존 gradeint descent에서는 세타에 (learning rate x gradient of loss function of 세타)를 빼주는 방식으로 매 스텝마다 세타를 업데이트 해주었는데, momentum에서는 세타에서 빼주는 term을 바꾸어주었다.
그 바꾸어준 값 vt는, 이전 스텝의 vt-1에 감마를 곱한 값과 , gradient descent에서 사용했던 (learning rate x gradient of loss function of 세타)의 합이다.
그리고 감마는 decaying constant이다.
감마가 없다면 vt는 이전의 vt값들을 더하면서 업데이트 되기에 계속 커질 것이다.
따라서 0~1사이의 감마값을 vt-1에 곱해주어, vt가 무작정 커지는 것을 방지한다.
vt를 씀으로서, 그 step에서의 gradient만을 계산하여 업데이트 하는 gradient descent 방식이 아닌, 매 step에서 누적된 gradient를 이용하여 업데이트 할 수 있고 이를 momentum(관성) 이라 한다.
Oscillating 란, 매 스텝마다 gradient가 통통 튀는 것을 뜻하는데, Gradient descent와 달리 모멘텀을 적용하면 누적된 gradient들을 이용하여, 보다 gradient가 통통 튀는 것을 어느정도 줄일 수 있고 convex로 들어가는 시간을 좀 더 줄일 수 있다.
Momentum의 단점은, 관성 떄문에, global minimum에 도착했다 하더라도 공이 이리저리 움직인다는 점이 있다.
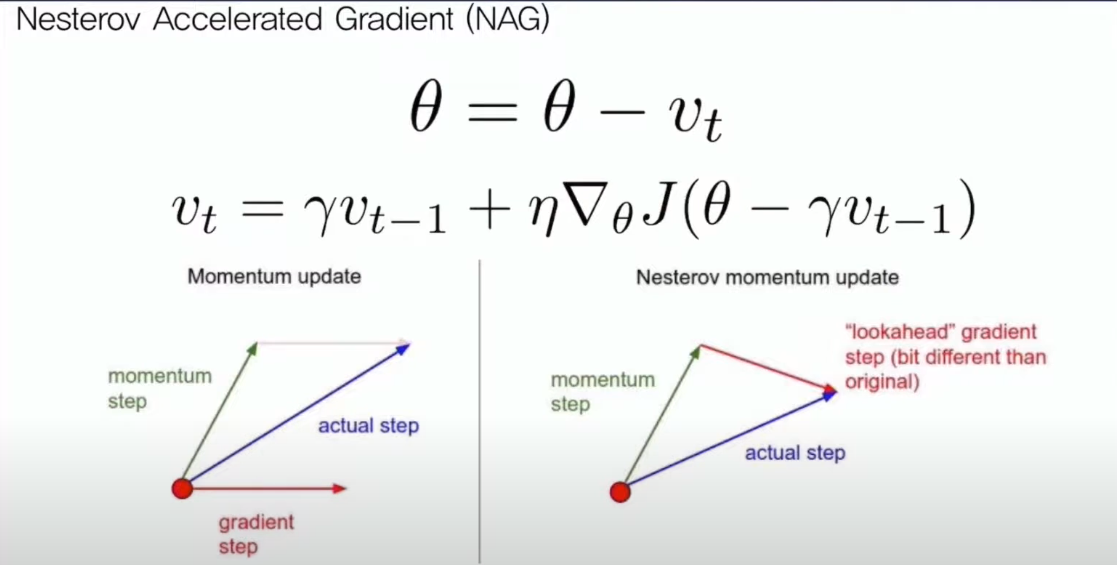
이를 해결한 방법이 NAG(Nesterov Acclerated Gradient)이다.
왼쪽을 보면 기존 momentum 방식은 앞서 누적되던 gradient들의 합과, 해당 step에서 구한 gradient를 합하여 step이 진행된다.
NAG는, step에서 momentum 즉 누적되던 gradient에 대해 update 연산을 하고, 그 연산된 점에서 gradient를 계산하여 연산하는 한 step이 2 stage로 이루어져있는 방식이다.
다시 말해 Momentum에 따른 변동사항을 먼저 적용시키고, 이후에 그것에 대한 gradient를 구하여 stepdmf 갱신을 시킨다는 개념이다.
결론적으로, local minimum을 피하기 위해 momentum이라는 개념을 더하고, 이를 진화시켜 convex에 더 빨리 수렴할 수 있도록 한 NAG가 위쪽 branch의 내용이다.
Adaptive learning
아래쪽 branch의 내용이다.
기존 SGD는 step 사이즈가 모든 파라미터에서 동일하다.
파라미터셋 세타가 {w1, w2, w3, w3 ,….}라고 할 떄, SGD를 통해 step을 돌며 다른 parameter들에 반해 w1만 계속 변했다면, w1은 minimum에 있을 확률이 크다.
그에 반해 w2, w3, w4는 그렇지 않다.
각 parameter마다 gradient는 다르지만, 앞에 곱해진 상수(learning rate)는 같다.
따라서 각각의 parameter마다, 다른 size(다른 크기의 learning rate)의 step을 밟아야 하는게 아니냐? 라는 개념이 주된 내용이고, 이를 adaptive learning 이라 한다.
Adagrad
Adaptive learning이 적용된 Adagrad이다.
수식을 설명하자면, gradient descent와 거의 비슷하지만, learning rate 밑에 새로운 term이 있다.
이 term은, 원래 Gt에, gradient의 제곱을 더한 값이다.
파라미터 셋 세타 안에 k 개의 parameter가 있다고 생각할 때, 각 parameter 별로 gradient 값을 제곱한 값을, Gt에 저장한다.
따라서 이 연산은 상수끼리의 곱이 아닌, elemental wise 한 벡터 연산 이다.(내적 dot product와 달리 벡터의 원소끼리만 곱함, 결과는 벡터)
뒤에 곱해지는 term 역시 k 개의 parameter에 대해 편미분 한 값을 쌓아둔 것임을 알 수 있다.( , , , ) 이런식으로..
다시말해 각 parameter 마다 곱해주는 learning rate값이 다르다.
이를 통해 학습에서 크게 변동이 있었던 가중치에 대해서는 학습률을 감소시키고 학습을 통해 아직 가중치의 변동이 별로 없었던 파라미터는 학습률을 증가시켜서 학습이 되게끔 한다.
즉 gradient(변해온 정도)에 반비례 하여 learning rate에 곱해준다.
(편미분한 gradient를, “변한 정도”라고 생각하기)
변동이 별로 없겄던 파라미터는, gradient가 작을 것이기에, 곱해지는 learning rate term이 다른 파라미터에 비해 클 것이다.
참고로 입실론은, 첫 step에서 0으로 나누어주면 안되기에 더하는 도구 개념이다.
Adagrad의 문제점은, G가 recursive하게 계속 더해지는 양수값이기에, G가 발산할 수 도 있다는 점이다.
따라서 나중의 step에서는 training을 오래 할 수록 곱해지는 learning rate가 매우 작아질 것이다.
RMSprop
이 곱해지는 learning rate term이 0으로 수렴하는 것을 막기위한 방법이 RMSprop 개념이다.
수식은 Adagrad와 비슷하지만, Gt에서 gradient 앞에 1 대신 (1-감마)가 곱해지는 것을 볼 수 있다.
Decaying constant를 이용하여 G가 발산하는 것을 막아주는 것을 볼 수 있다.
Adam
Momentum 개념과, adagrad 개념을 합친, Adam optimizer(Adaptive Moment Estimation)이다.
m 은 momentum 개념, v는 adaptive learning에서 나온 개념이다.
첫 줄은 앞서 본 gradient의 관성을 유지하는 momentum에 대한 수식이다.
그리고 두번째 줄은 각 파라미터 당 learning rate를 다르게 주기 위한 Adagrad에 관련된 내용이다.
실제 task에 적용시 베타1dms 0.9, 베타 2는 0.99의 값을 갖는데, 첫 스텝에서는 mt-1, vt-1이 없으므로 셋 째 줄을 이용한다.
따라서 앞서 설명한 내용들을 종합하면, Momentum 개념과 adagrad 개념을 합친 ADAM optimizer를 이해 할 수 있다.
Subscribe via RSS