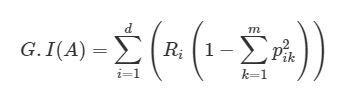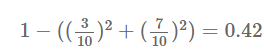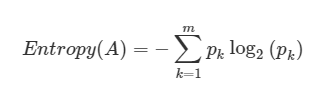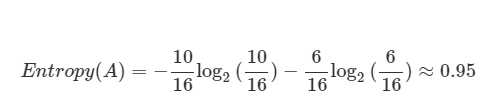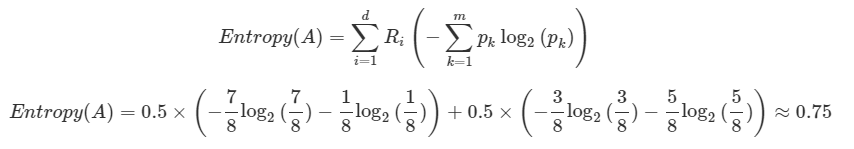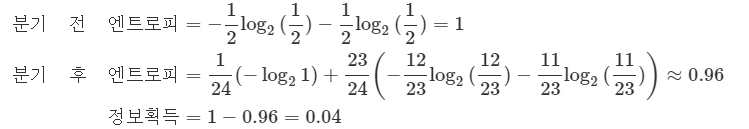의사 결정 트리
by
의사 결정 트리
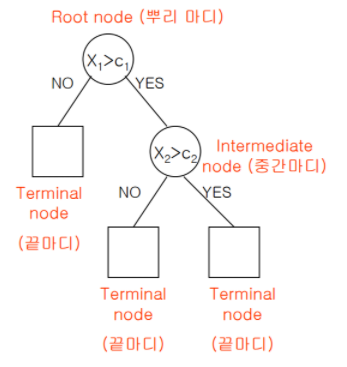
의사 결정 트리란 데이터를 분석하고 이들 사이 존재하는 패턴을 규칙들의 조합으로 나타내는 것이다.
동그라미를 노드, 네모를 각 가지 (leaf)라 한다.
본 노드를 2의 깊이를 가지고 있다. 라고 나타낼 수 있고, 4개 (사실은 3개)리프를 가지고 있다. 라고도 표현한다.
균형 이진 트리에서 깊이 d의 리프 노드의 개수는 2^d 이다.
깊이가 2이기에, leaf는 2^2개를 갖는 것이고, 시간복잡도로는 O(log2(leaf))인 O(log2(4)) 의 값을 갖는다고 할 수 있다.
분기가 거듭될 수록 각 리프에 해당되는 데이터의 갯수는 줄어들고, 모든 리프에 있는 데이터를 더하면 루트 노드에 있는 데이터 개수와 같아진다.
의사 결정 트리에서는 분류, 회귀 역시 가능하다.
분류는 데이터가 주어질 떄 같이 주어진 (노드를 통해 판별할 수 있는) 조건을 통해 할 수 있다.
회귀의 경우 트리를 순회하여 리프노드에 도달 후, 그 리프 노드에 있는 수많은 훈련 샘플들의 평균 타깃 값이 예측값이 된다.
불순도와 불확실성
이진 트리의 학습 방향은 다음과 같다.
1. 순도 (homogeneity) 증가
2. 불순도(impurity), 불확실성(uncertainty) 감소
다음의 학습을 정보 획득 이라고도 한다.
이 중 불순도 지표인 지니 계수와, 불확실성의 지표인 엔트로피에 관한 설명이다.
먼저 지니 계수의 공식이다.
지니불순도는 데이터 분석에서 이진 트리에서 사용되는 클래스 개수에 따른 케이스들의 불순한 정도를 나타내는 척도이다.
Pi,k는, i번째 노드에 있는 훈련 샘플 중 클래스 k에 속한 샘플의 비율을 나타낸다.
구슬 10개 중 파란 구슬이 3개, 빨간 구슬이 7개 있다고 할 떄 지니 계수를 구하면,
다음과 같이 42%의 지니 불순도를 갖는다.
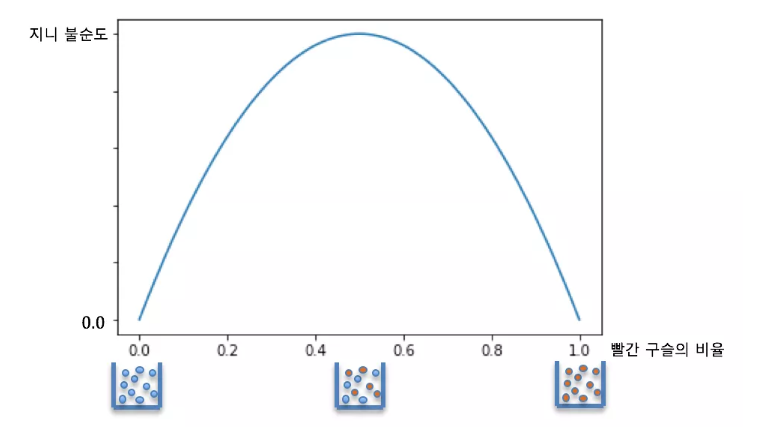
구슬이 파랑 5개, 빨강 5개 있을 떄 불순도가 최대임을 알 수 있다.
다음은 엔트로피 이다.
엔트로피는 다음과 같은 식을 갖는다.
m개의 데이터가 속하는 A 영역에 대한 엔트로피를 나타낸 식이다.
여기서 pk는 A영역 내 속하는 데이터 가운데 k범주에 속하는 데이터 비율이다.
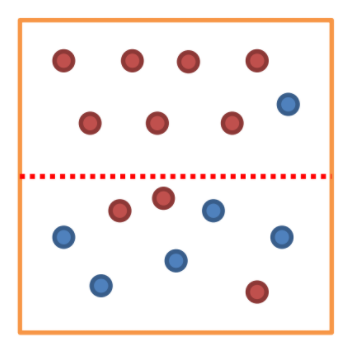
여기서 m 은 빨강 + 파랑인 16 이고, 범주 1에 해당되는 빨간 동그라미는 10, 범주 2에 해당하는 파랑 동그라미는 6이므로 A의 엔트로피는 다음과 같다.
(로그의 밑이 2이기에, 각 term 앞에 -가 붙은 모습을 알 수 있다.)
이 떄 이어서 가운데를 영역 A라고 놓고 빨간 실선을 그어서 또 엔트로피를 구해보면, 다음과 같다.
Ri는 i 영역에 속하는 데이터 개수/분할 전 데이터 개수로, 각각 8/16으로 1/2임을 알 수 있다.
앞 term은 A로 먼저 범주를 나눈 후, 윗 범주에 대해 빨강/파랑으로 범주를 나눈 값 이고
뒤 term은 A로 범주를 나눈 후, 아랫 범주에 대해 빨강/파랑으로 범주를 나눈 값임을 알 수 있다.
이를 깊이가 2인 이진트리라고도 추측해 볼 수 있다.
엔트로피 값을 보면 알 수 있듯이, 불확실성이 많이 줄어든 모습이다.
만약 구슬 10개라면 파랑 5개, 빨강 5개 있을 떄 엔트로피는 최대(1) 임을 알 수 있다.
지니 불순도와 엔트로피 중 어떤 것을 사용하든 큰 차이가 없지만, 지니 불순도가 조금 더 계산이 빠르기에 기본값으로 좋다고 한다.
재귀적 분기와 가지치기
모델 학습과정의 차이에 따라 나뉘는 두 case이다.
재귀적 분기의 부터 살펴보겠다.
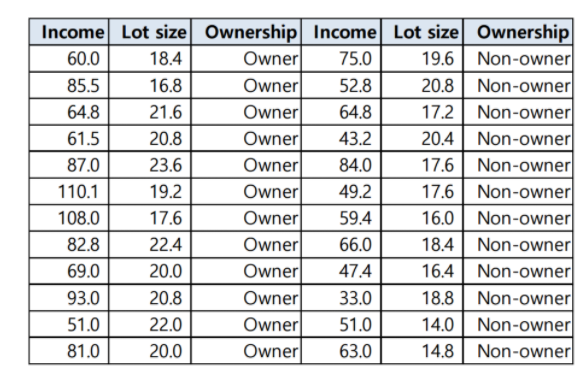
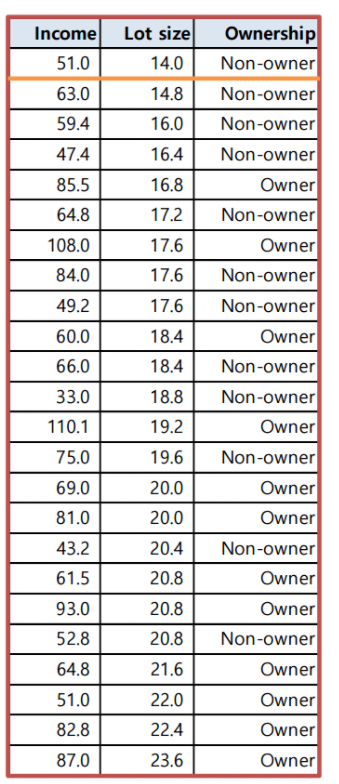
맨 위 사진은 Y(종속 변수) = 구입여부, X(설명 변수) = 소득, 주택크기로 하고 표로 정리한 모습이다.
두 번쨰 사진은 X중 하나인 주택크기로 오름차순 정렬하여 표로 나타낸 모습이다.
이 표를 주택크기가 가장 적은 맨 위 항목(항목 1)과 나머지 항목(항목 2~ 항목 24)으로 범주를 나눈 후, 구입 여부인 Y에 대해 범주를 나누어 엔트로피를 구한 결과는 다음과 같다.
재귀적 분기란 본 분기를 항목 2와 나머지에 대해, 항목 3과 나머지에 대해.. 를 반복하여 정보획득이 높은 분기점(항목) 을 찾아나가는 과정이다.
따라서 개체가 n개, 변수가 d개라 할 떄 분기를 위해 해야 할 경우의 수는 d(n-1)개라 할 수 있다.
두 번째 학습 방법은 가지치기 이다.
쉽게 말해 오버 피팅을 방지하기 위해 노드들을 가지치기 하는 것이다.
분기가 많으면 일반화시 성능이 오히려 더 떨어진다.
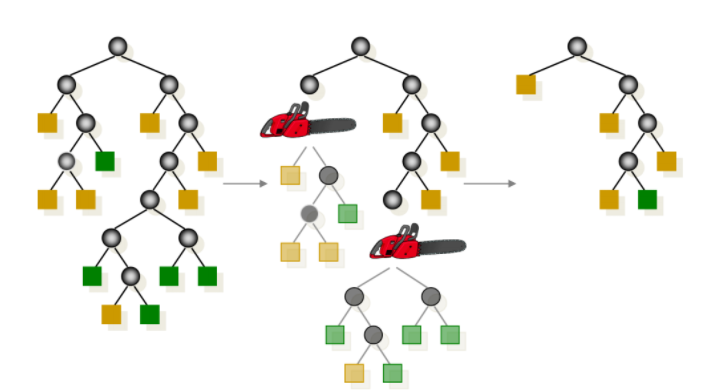
가지치기 한다 라는 표현은 혼동을 줄 수 있는데, 각 분기를 버리는 것이 아니라 분기를 합친다고 이해햐면 된다.
다음 그림은 노드를 가지치기 했을떄, 그렇지 않았을 때의 성능평가이다.
추가 내용 - 모델 정의

다음은 이진 트리 모델을 함수 형태로 나타낸 모습이다.
I 는 indicater function으로, 괄호 안의 값이 맞으면 1, 아니면 0 값을 뱉어주는 함수이다.
그리고 맨 위 term의 중괄호 내 내용의 의미는, “(x1, x2)가 R1영역 내에 있느냐?” 라는걸 내용이다.
만약 새로운 숫자 (x1, x2)가 R3영역에 속한다면, 예측값인 f^(x)의 값은, 상수 cm의 값을 가지게 될 것이다.

최상의 분할에 대해 살펴본다.
끝마디가 m개인 f(x)에 대해, 상수인 cm을 구하는 것이 목표이다.
yi는 실제 값이고, fx1은 모델의 예측 값이다.
이 둘의 차이를 최소화 하는 cm (시그마 term값을 최소로 하는 cm)을 찾는 것인데, 이 cm은 각 분할에 속해 있는 y값들의 평균일 떄 loss function이 최소의 값을 갖는다.
즉 최상의 분할을 한다.
추가 내용 - 분할점과 분할변수

분할 기준이 x1 < 2일 떄, 분할변수 j는 1이고 분할점 s는 2이다.
왜 분할변수를 j를 1로 사용하고 분할점을 2로 사용하는지 방법론에 관한 이야기이다.
argmin[]은 [] 의 값이 최소가 되게 하는 j,s 값을 의미한다.
맨 위 수식의 [] 값은, 앞선 모델 정의에서 시그마 term(비용함수)가 최소가 되기 위해서는 cm은 각 분할에 속해있는 y값 들의 평균이라는 값을 도출했었다.
좀 더 자세히 말하자면 예를 들어 X1 <= 2의 를 갖는 영역을 R1, X1 > 2를 갖는 영역을 R2라 할 때, c1, c2는 각각 그 분할에 속해있는 값 들의 평균값 이다.
예를 들어
분할 변수는 x1, 그 때 분할점은 2 or 3
분할 변수는 x2, 그 때 분할점은 4 or 5
분할 변수는 x3, 그 때 분할점은 6 or 7
인 경우가 있을 떄, 위 task의 총 경우의 수는 6가지 이다.
6가지의 경우의 수 중 [ ] term을 최소화 하는 한 경우의 수를 골르고 그 때 j, s을 구하는 것이다.
즉 분할점과 분할변수란 두 번쨰 argmin 식에서 [ ]term을 최소화 해주는 기준인 R1, R2를 정하는 척도인 j, s를 찾는 내용이다.
참고로, agrmin을 통해 모든 경우의 수에 대해 찾으므로, 이는 greedy search라 할 수 있다.
결론
사결정나무는 계산복잡성 대비 높은 예측 성능을 내는 것으로 유명하다.
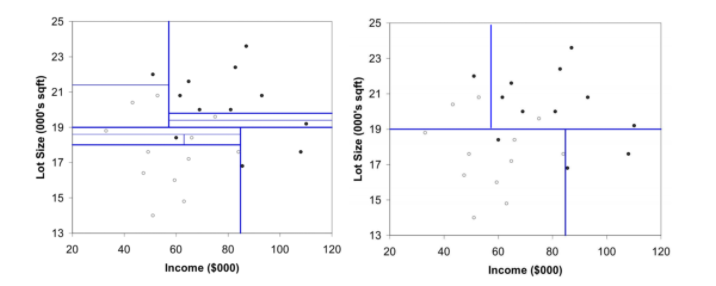
다만 의사결정나무는 결정경계(decision boundary)가 데이터 축에 수직이어서, 데이터가 좀만 회전된 경우 등에는, 적절히 작동하지 못한다.
이는 랜덤포레스트를 통해 보완이 가능하다.
아직 강의 [1]만 보고 [2]는 안봤음.
Subscribe via RSS