Algorithm-3 Time complexity by Algorithms
by
https://blog.naver.com/kbs4674/220727498080
Heap이란?
여러개의 값들 중 최대값이나 최솟값을 빠르게 찾아내도록 만든 자료구조이다.
이진트리와 달리 중복된 값을 허용한다.
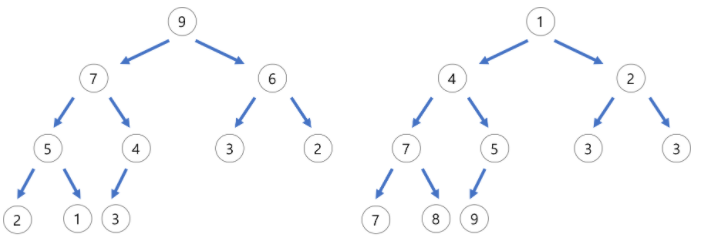
부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같으면 최대 힙(좌측), 부모 노드의 키 값이 자식노드보다 작으면 최소 힙 이라 한다.
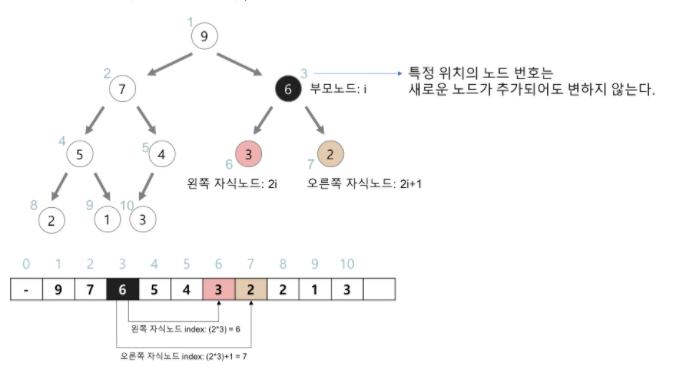
힙은 배열의 자료구조로 저장된다.
특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않고, 이는 그림을 통해 직관적으로 알 수 있다.
힙에서 부모 노드는, 자식 노드의 인덱스를 2로 나눈 몫이다.
다음은 Max heap이다.
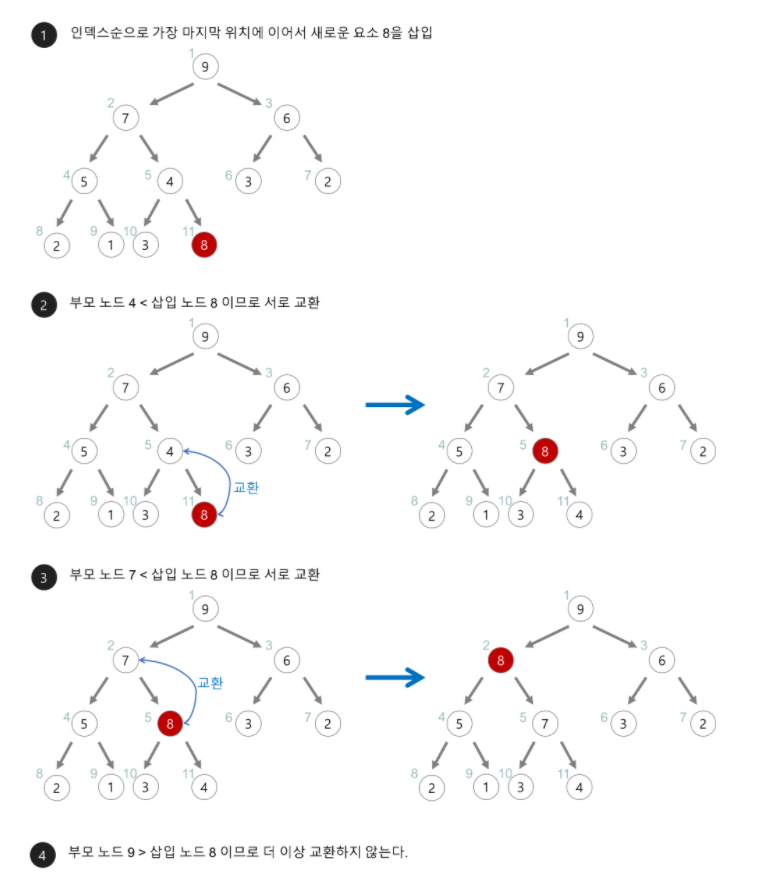
heap에 새로운 요소가 들어오면 힙의 마지막 노드에 삽입하고 부모노드와 크기를 비교하여 교환 여부를 따진다.
부모 노드보다 크다면 부모 노드와 교환하고 인덱스도 서로 바꾸어준다.
Insertion sort
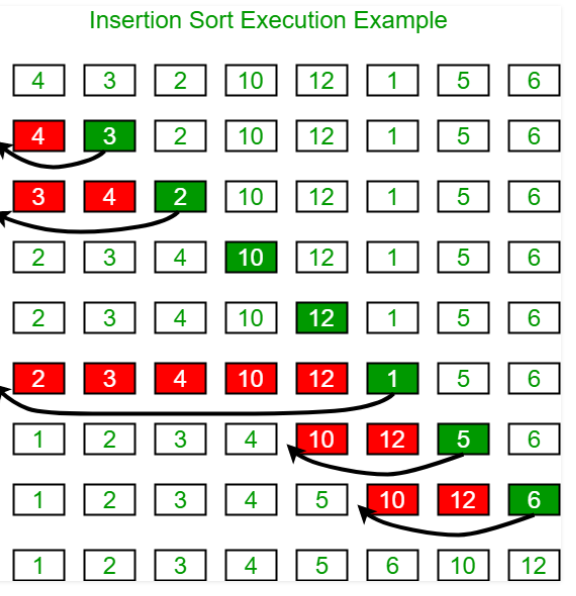
Insertion sort는, 두 번 째 element(key) 부터 시작한다.
그 앞 element와 비교하여 key 값 보다 크기가 크면 그 자료의 위치에 key를 배치하는 작업을 key 값보다 크기가 작은 자료를 만날 떄 까지 반복한다.
O(n^2)의 worst time complexity를 갖는다.
이유 : element가 n 개인 배열일 때, 걸리는 worst time은
1 + 2 + 3 + … (n-2) + (n-1) = n(n-1)/2 즉 O(N^2)가 된다.
빅 오 표기법은 시간의 상한 즉 최악으로 걸리는 시간을 나타내는데 사용한다.
이미 정렬되어 있다면 효율적인 알고리즘이다.
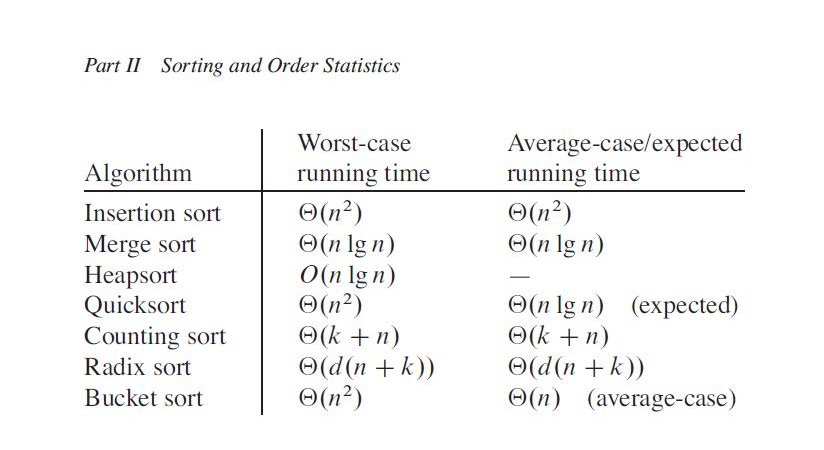
알고리즘 별 시간 복잡도
여기서 빅 세타()는 점근적으로 근접한 값(괄호 안의 값) 을 갖는다는 의미이고,
빅 오()는 최대(최악)으로 걸리는 값으로 괄호안의 값을 갖는 다는 의미이다.
Merge sort
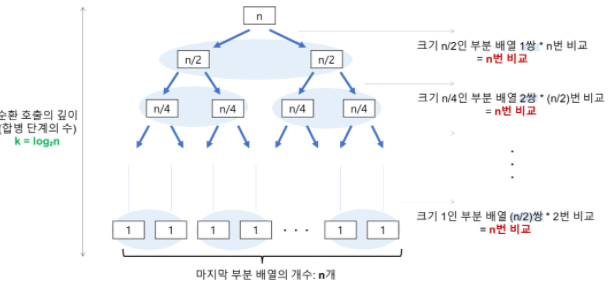
merge sort는 반으로 쪼개고 합쳐서 정렬하는 알고리즘이다.
반으로 쪼개는 수행 시간은 element가 N 개일 때 logN 이다.(밑 = 2)(쪼개는데 걸리는 시간만 생각한다.)
그리고 정렬 자체에 걸리는 시간은 N 이다.
1 번째 row 에서 2번쨰 row로 갈 때, 좌측 덩어리와 우측 덩어리로 나누어, (6, 5) 에 대한 비교 -> (6, 8) -> (7, 8) 즉 element 개수가 4개 일 때 연산 횟수도 4번 이다.
이러한 방식으로 인해 정렬에는 N 의 수행 시간이 걸린다.
최적, 평균, 최악 모두 큰 차이 없이 O(nlogn)의 시간복잡도를 갖는다.
Heap sort
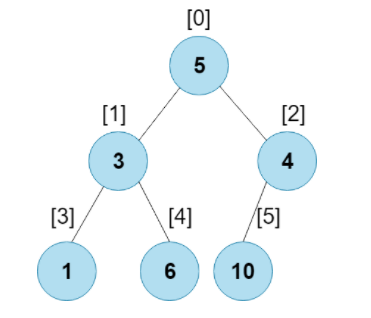
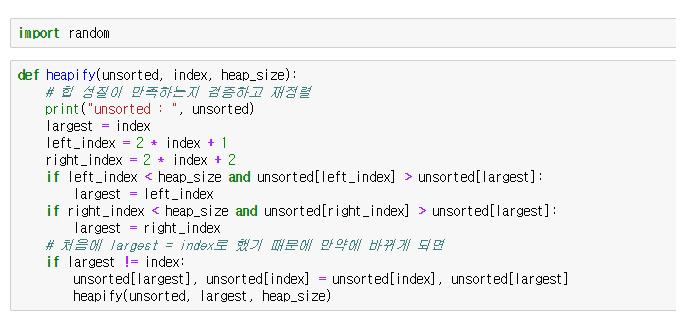
Heap sort를 하기 위해선, 최대 heap을 만들어 주기 위한 heapify 작업이 필요하다.
아래와 같은 heap을 최대 heap으로 만들어 주는 작업이다.
위 코드로 maxheap 구조를 만들 수 있고 이 때 수행 시간은 O(logN) 이 걸린다.
두 번째로 heap sort를 하는 부분인데, 이 부분은 heap을 내림차순으로 정렬해 주는 부분이다.
자세한 내용은 https://zeddios.tistory.com/56 참고.
Max heap을 만들어 주는 시간복잡도는 한 번 자식 노드로 내려갈 때 마다 노드의 갯수가 2배씩 증가함으로 O(logN)이다.
그리고 전체 데이터의 갯수가 N개이므로 정렬을 하는데 필요한 시간은 N,
힙 구조를 만드는 종합적인 시간복잡도는 O(NlogN)으로 볼 수 있다.
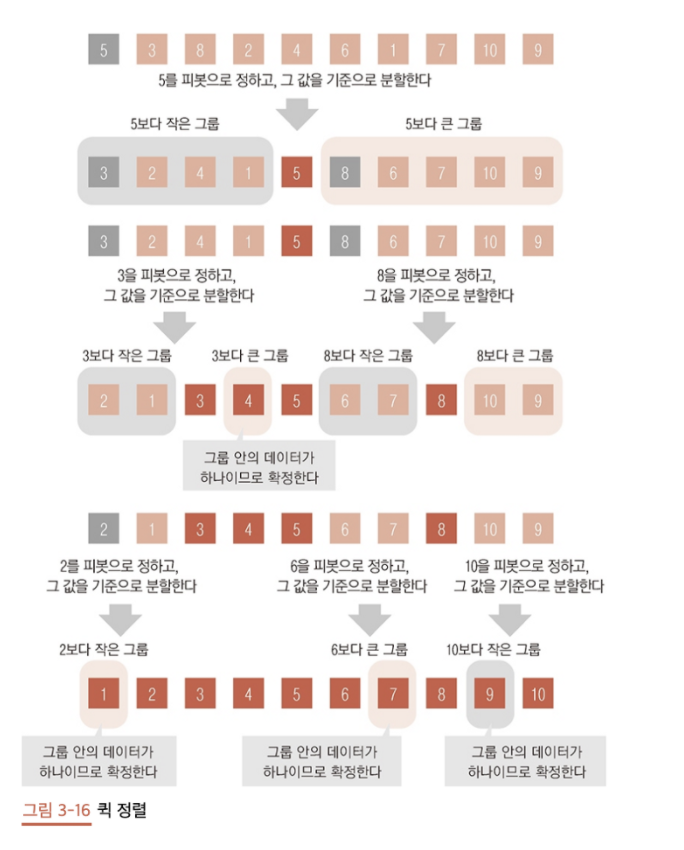
Quick sort
https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html 참고
첫번째 값(5)을 피벗으로 택한다.
이 값보다 작은 값들로만 구성된 리스트와 큰 값들로만 구성된 리스트 둘로 분할한다. (이를 각각 LESSOR와 GREATER라고 명명)
LESSOR와 GREATER 각각에 같은 작업을 해당 리스트의 요소 개수가 하나가 될 때까지 재귀적으로 반복
https://ratsgo.github.io/data%20structure&algorithm/2017/09/28/quicksort/
Worst time complexity로 O(N^2)를 갖지만, 평균적으로는 O(NlgN) 값을 갖는다.
정렬된 리스트에 대해서는 오히려 시간이 더 필요하다.
Code
import time
from numpy.random import seed
from numpy.random import randint
import matplotlib.pyplot as plt
import numpy as np
import sys
#/////////////////재귀한도 깊이 설정
def func(n):
if n == 1500:
return
func(n + 1)
if __name__=='__main__':
sys.setrecursionlimit(2000)
func(1)
#/////////////////재귀한도 깊이 설정
def Insertion_Sort(array):
for a in range(1, len(array)):
for b in range(a, 0, -1):
if array[b] < array[b-1]:
array[b], array[b-1] = array[b-1], array[b]
else:
break
return array
def merge(left, right):
result = []
while len(left) > 0 or len(right) > 0:
if len(left) > 0 and len(right) > 0:
if left[0] <= right[0]:
result.append(left[0])
left = left[1:]
else:
result.append(right[0])
right = right[1:]
elif len(left) > 0:
result.append(left[0])
left = left[1:]
elif len(right) > 0:
result.append(right[0])
right = right[1:]
return result
def merge_sort(unsorted_list):
if len(unsorted_list) <= 1:
return unsorted_list
mid = len(unsorted_list)//2
left = unsorted_list[:mid]
right = unsorted_list[mid:]
left1 = merge_sort(left)
right1 = merge_sort(right)
return merge(left1, right1)
def heapify(unsorted, index, heap_size): #max heap 만들기
largest = index
left_index = 2*index + 1
right_index = 2*index + 2
if left_index < heap_size and unsorted[left_index] > unsorted[largest]:
largest = left_index
if right_index < heap_size and unsorted[right_index] > unsorted[largest]:
largest = right_index
if largest != index :
unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest]
heapify(unsorted, largest, heap_size)
def heap_sort(unsorted):
n = len(unsorted)
for i in range(n//2 -1, -1, -1):
heapify(unsorted, i, n)
for i in range(n-1, 0, -1):
unsorted[0], unsorted[i] = unsorted[i], unsorted[0]
heapify(unsorted, 0, i)
return unsorted
def quick_sort(ARRAY):
ARRAY_LENGTH = len(ARRAY)
if( ARRAY_LENGTH <= 1):
return ARRAY
else:
PIVOT = ARRAY[0]
GREATER = [ element for element in ARRAY[1:] if element > PIVOT ]
LESSER = [ element for element in ARRAY[1:] if element <= PIVOT ]
return quick_sort(LESSER) + [PIVOT] + quick_sort(GREATER)
#Test Code
elements_insertion = list()
elements_merge = list()
elements_heap = list()
elements_quick = list()
times_insertion = list()
times_merge = list()
times_heap = list()
times_quick = list()
iteration = 20
for i in range(1, iteration):
#a = randint(0, 1000 * i, 1000 * i)
a = np.array(range(100 * i, 0, -1))
start = time.clock()
#Insertion_Sort(a)
end = time.clock()
print(len(a), "Elements Sorted by InsertionSort in ", end-start)
elements_insertion.append(len(a))
times_insertion.append(end-start)
for i in range(1, iteration):
#a = randint(0, 1000 * i, 1000 * i)
a = np.array(range(100 * i, 0, -1))
start = time.clock()
merge_sort(a)
end = time.clock()
elements_merge.append(len(a))
times_merge.append(end-start)
print(len(a), "Elements Sorted by mergeSort in ", end-start)
for i in range(1, iteration):
#b = randint(0, 1000 * i, 1000 * i)
b = np.array(range(100 * i, 0, -1))
start = time.clock()
heap_sort(b)
end = time.clock()
elements_heap.append(len(b))
times_heap.append(end-start)
print(len(b), "Elements Sorted by HeapSort in ", end-start)
for i in range(1, iteration):
#b = randint(0, 1000 * i, 1000 * i)
b = np.array(range(100 * i, 0, -1))
start = time.clock()
quick_sort(b)
end = time.clock()
elements_quick.append(len(b))
times_quick.append(end-start)
print(len(b), "Elements Sorted by QuickSort in ", end-start)
plt.xlabel('List Length')
plt.ylabel('Time Complexity')
plt.plot(elements_insertion, times_insertion, label ='Insertion Sort')
plt.plot(elements_merge, times_merge, label ='Merge Sort')
plt.plot(elements_heap, times_heap, label ='Heap Sort')
plt.plot(elements_quick, times_quick, label ='Quick Sort')
plt.grid()
plt.legend()
plt.show()
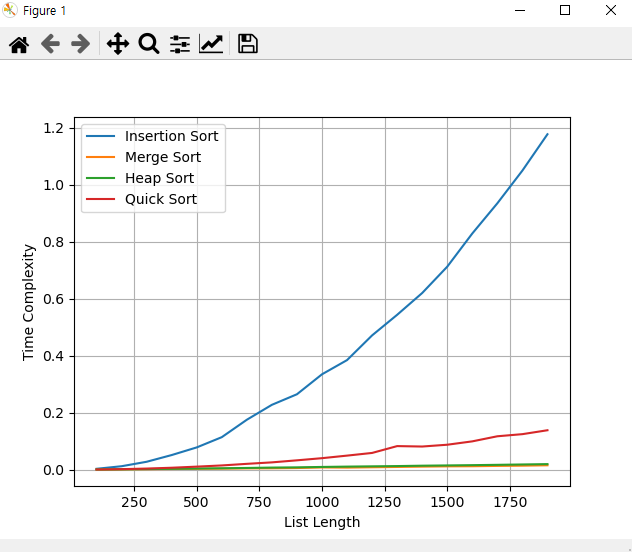
결과비교 - insertion sort 포함 네 알고리즘의 worst time complexity 비교
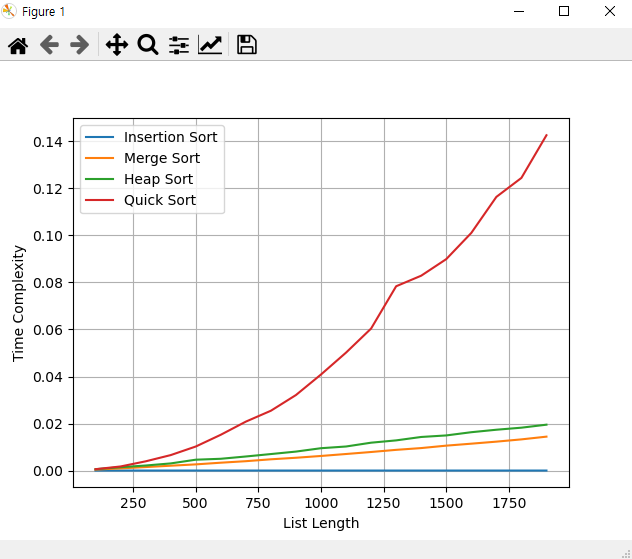
결과비교 - insertion sort 제외 세 알고리즘의 worst time complexity 비교
Subscribe via RSS