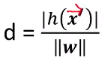Support Vector Machine

8-1

1. SVM이란?

머신러닝 중 가장 유명하고 널리쓰이는 알고리즘이다.

구현이 간단하고, 효율성 있다는 특징이 있다.

Classification 에 주로 쓰이고, 기존 존재한 Logistic regression, clustering과 달리 boundry를 침으로써 classify한다는 특성이 있다.

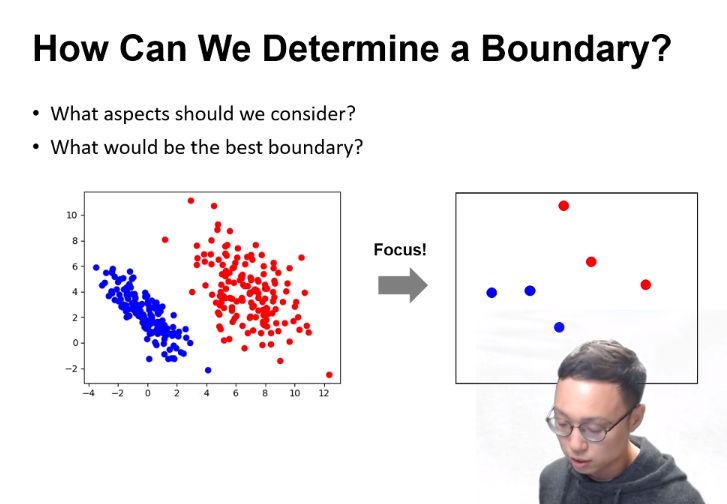
1-1. SVM - classification boundary

Boundary를 칠 때, 모든 data가 아닌 애매한, 기준이 될 data만을 추출하여 boundary를 치는것이 연산상 효율적일 것이다.

기울기와 점(위치)만 정해줄 수 있다면, boundary line을 그릴 수 있을 것이다.

따라서 기울기, 위치(점)에 대한 기준점만 주어지면 된다.

기울기와 위치를 한 번에 정하기 힘드니, 1. 기울기 고정 후 점 구하기 2. 점 고정 후 기울기 구하기로 step을 나누어 보자.

기울기가 정해졌을 때, 최적의 (line)위치를 찾는 경우 : 가장 가운데에 있는 line이 desirable 할 것이다.

파란점, 빨간 점 두 점과 line간의 거리가 가장 긴 지점이 line이 될 것이다.

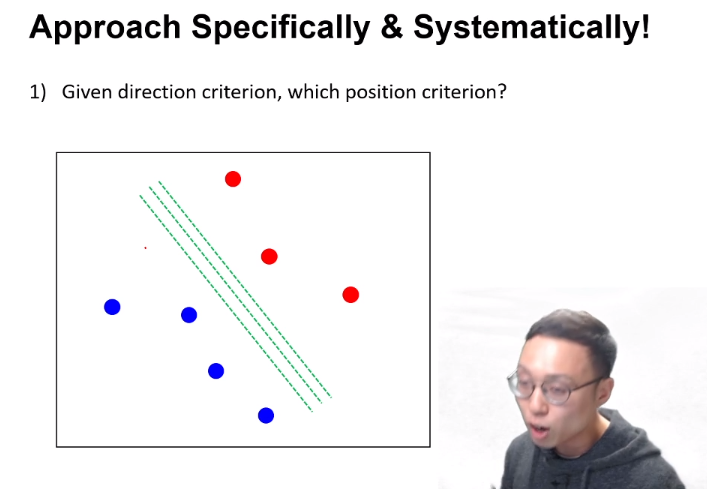
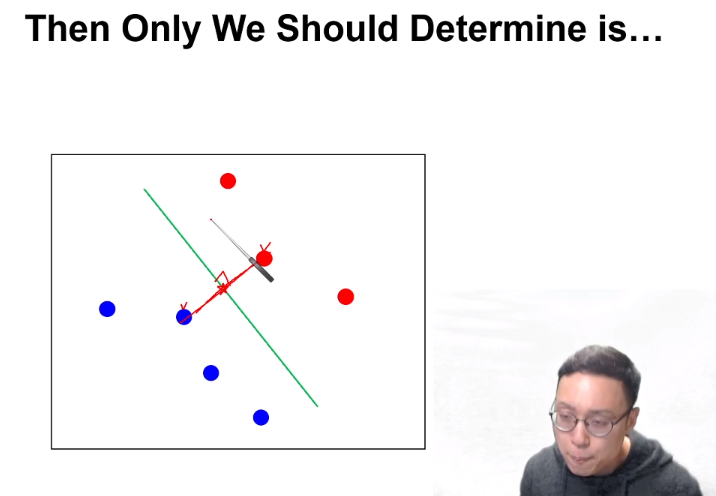
위치가 정해졌고 기울기를 정해야 하는 경우 :

파란, 빨간 점과 선 간의 왔다갔다 하는 거리가 먼 초록색 line이 보라색 line보다 좋은 criterion일 것이다.

즉 margin을 maximize하는 line일 것이다.

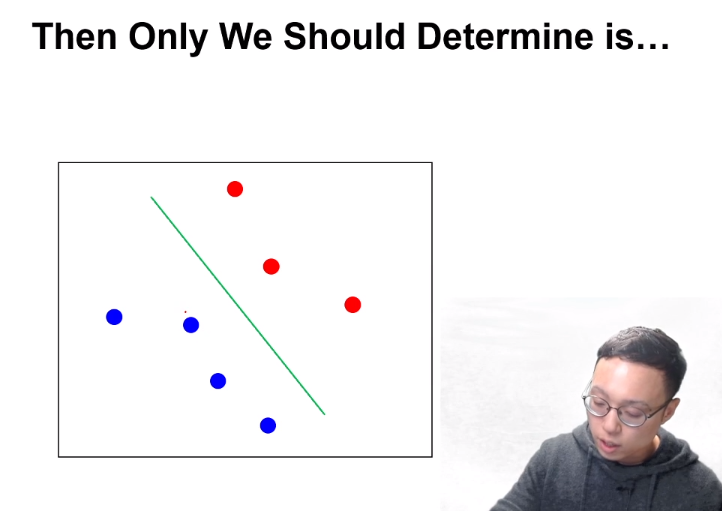
따라서 저 초록색 line을 구하려면, 가장 가까운 거리의 파랑, 빨강 점의 중점을 지나면서 그 두 점을 이은 벡터에 수직인 직선을 구하면 optimal한 boundary가 될 것이다.

다른 점은 다 필요 없다는 의미이다.

이때 저 두 point를 support vector라고 한다.

하지만 세상에는 linearly seperable 하지 않은 data가 너무 많고, 이를 Kernel trick, 라그랑쥬 승수법을 통해 해결한다.

8-2

2. Kernel Trick

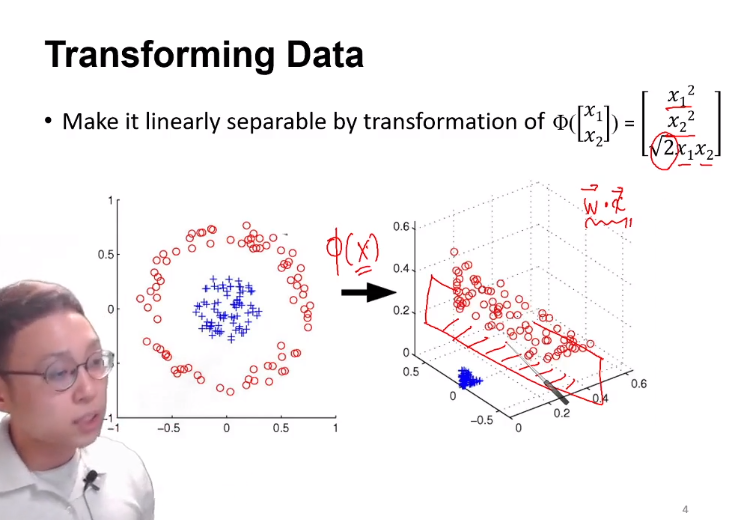
2-1. linearly inseperable한 data 를 seperable하게 분리하는 방법

다음과 같은 식을 통해 boundary를 linearly seperable하도록 차원을 증가시켜 주어 classify할 수 있다.

이 고차원으로 변형시켜주는 식을 mapping function Φ 라고 한다.

하지만 이렇게 차원을 무조건적으로 증가시켜주면, computational power 역시 증가하여 단점이 있을 것이다.

차원은 높이되 계산량을 높이지 않는 방법은 없을까?에서 등장한 개념이 kernel trick이다.

2-2. Kernel trick

(Q(transformed space R) » P(original space R)) Mapping function을 통해 high dimension으로 transform된(Q차원) Φ(x)를 Φ(x’)와 내적한 값은 매우 complex한 계산을 거치지만 결국 scalar값을 가질 것이다.

이를 K(x, x’)라는 특정 함수를 통해 P라는 original space에서 구할 수 있다면, 연산량은 매우 적어질 것이다.

이 K라는 function을, kernel function이라 한다.

다음은 kernel function의 예이다.

만약 mapping function으로 x, y를 transform하고 그 두 값을 내적한 값이, original space에서 kernel function에 x, y 값을 대입만 해준 경우와 똑같다면, 연산량이 매우 줄어들 것이다.

Mapping function이 주어지지 않았더라도, kernel function만 주어졌다면, classify가 가능하다.

우리가 계산시에는, 고차원의 내적된 값만 필요할 뿐 저차원에서 어떻게 mapping되고 ~ history는 필요가 없다.

오로지 kernel function을 통해 계산된 (= mapping function에서 내적한) scalar값만이 중요하다.

위 그림은 어떤 mapping function을 쓰냐에 따라 달라지는 kernel function들이다.

그 중 RBF kernel을 매우 자주쓰는데, 이 function이 왜 effective한지는 다음 이유와 같다.

kernel function이 주어졌을 때, taylor expansion을 통해 mapping function을 예측한 슬라이드이다.

Ridge regression의 경우 line이 data에 너무 fit 되다보면 wiggle거리는 경우가 많은데, 이를 input data의 차원을 kernel trick을 통해 높여주면, 고차원 상에서 ridge regression이 적용된 형태일 것이므로 wiggle거림이 해소될 것이다.

8.3

3. Lagrange Multiplier

3.1 Lagrange multiplier이란?

Contraint가 주어졌을 때 optimize하는데 매우 powerful한 tool이다.

Implicit function expression
한국어로는 음함수로의 표현 이다.

y = 3x + 5(양함수) 를,

y - 3x - 5 = 0

꼴과 같이 f(x, y) = 0 꼴로 쓰는 것이다.

Gradient
Gradient란, 변수가 여러개인 함수에 대해서, 각 변수에 대해 partial differential 해주어 벡터 꼴로 나타내준 것이다.

위의 f(x, y)를 gradient 해주면 (-3, 1)이다.

Gradient는, 기하학 적으로 해당 함수를 가장 크게 변화시키는 방향을 의미한다.

3-2. Constraint가 등식일 때

g(x)가 constraint이고, f(x)를 maximize해야 한다고 할때,

g(x) 와 f(x)의 gradient가 같다(평행하다)면 그 점이 최대 혹은 최소인 점일 것이다.

즉,

f = λ∇g
constraint : g(x) = 0

를 수학적인 편의성을 위해서 동시에 써준 것이 라그랑쥬 승수법이라 할 수 있다.

constraint와 objective를 merge한 식을 auxiliart function(L)이라 하고 이는 위 그림에 있다.

위 L을, x, y 그리고 λ에 대해서 gradient 하였을 시 0인 점을 찾으면, 그 지점은 최소 혹은 최대인 점일 것이다.

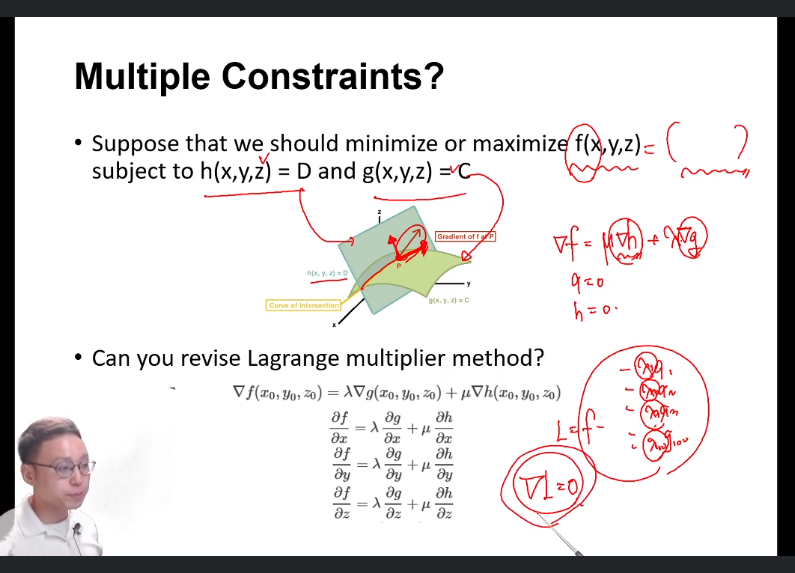
만약 constraint가 여러개 라면, 즉 g에 더해 h라는 constraint까지 만족해야 한다라면,

h를 초록색, g를 연두색 평면이라 할때 두 평면의 교선이 constraint일 것이다.

그리고 그 교선중에 f를 최대화 하는 점이 있을 것이다 (찾아야 한다)

h의 gradient, g의 gradient가 다음과 같을 때 그 gradient간의 linear combination인 gradient가, f를 최대화 하도록 만족시킬 것이다.

즉,

g(x, y, z) = 0

h(x, y, z) = 0

그리고 저 linear conbination 을 뺀 식이 0일 것이 될 때 f가 최댓값을 갖는다.

3-2. Constraint가 부등식일 때

∇f = λ∇g
constraint : g(x) <= 0

에 더하여,

mg(x*) = 0
m >= 0

까지 만족시켜야 한다.

3-2.3. 의 의미

f가 최소일때의 좌표를 x*라 할 때,

조건 1 : 위 그림은 constraint g(x) <= 0 가 f가 x*를 포함한다.

따라서 f(x)에만 집중하여 minimum point를 찾아야 하므로 constraint가 의미가 없다.

조건 2 : 반대로 아래 그림에서는 x*가 constraint에 포함되어 있지 않으므로, 즉 차선인 g(x)의 경계선(boundary)에 x^가 있을 것이다.

즉

조건 1 :

L = f + mg(x) 에서 g(x)를 아예 고려하지 x (m = 0으로 두어주면 됨)

조건 2 :

g(x) = 0 (m > 0으로 두어주면 됨, g(x) = 0)

이 두 조건을 한 식으로 표현하면, mg(x*) = 0이다.

3-2.4. 의 의미

gradient는 가장 큰 값으로 변화하는 방향을 의미한다.

즉 3.2.3 - 조건1 은 해당 되지 않고(constraint를 고려하지 않으므로 gradient 비교할수 x) 조건 2만 해당된다.

조건 2를 살펴보면,

boundary 조건에서 minimal 조건이 찾아지는 것이기에, 내 영역 내에는 global minimal 가 없다.

이 때 f의 관점으로 볼 때, ∇f 가 색깔 boundary 안으로 들어가는 방향이 f가 증가하는 방향이다.(boundary 바깥에 global minimum이 있으니깐)

g의 관점에서 볼 때는, g(x) > 0은 boundary 바깥 영역이다. (그림보고 이해하기)

따라서 g(x)가 증가하는 방향(∇g)은 boundary 바깥으로 나가는 방향이다.

따라서 ∇f와 ∇g는 부호가 반대이다.

∇L = ∇f + ∇mg(x) = 0에서

f, g의 부호가 반대임을 표시하려면

∇f = -∇mg(x)로 두어준다.

만약 constraint가 여러개라면,

와 같이 앞에 sigma만 붙여주면 된다.

위 조건을 KKT condition이라 부른다.

f(x)를 minmize한다는것에 꼭 주목.. maximize이면 부호 반대.

9.1

4. SVM

앞서, margin을 최대화 하는 방식으로 boundary를 정한다라고 하였다.

이를 위해

수학적으로 margin을 표현
미분을 통해 margin을 최대화

하는 과정을 하려 한다.

먼저, 1을 살펴볼 것인데, 이때 data는 linearly seperable하다고 하자.

새로운 data x = (x1, x2)가 들어오면, h(x) boundary에 대입하여, x>0이면 위쪽, x<0이면 아래쪽 으로 분류한다.

이때 w의 graphically meaning을 살펴보자.

이 w는, 해당 h(x) hyperplane에 수직인 벡터(normal vector)를 의미한다.

또한 w는, 특정 값만 갖는게 아니라 k값에 따라 다음과 같은 두 식으로 표현 가능하다.

다시말해 어떤 값으로 k값을 정하든, final result에는 영향이 없다.

만약 h(x) 외부의 특정 점 x0의 h(x0)값이 특정 값 h0을 갖고자 하면, 이 때 만족하는 w는 딱 하나밖에 없다.

이 h(x)식을 h0로 나누면 깔금하게 표현할 수 있다.

4-1. margin의 mathmetically하게 표현하기

x’ = h(x) 위의 점, x = h(x) 외부의 점

h(x) 외부의 점 x에서 직선까지의 거리는, 다음과 같이 d를 통해 나타낼 수 있다.

(혼자 해보기)

뜻 : 외부의 점 x를 내 hyperplane식에 넣고, normal vector 크기로 나누어준것.

이는 곧 boundary로부터 support vector까지의 거리를 구할수 있다와 동치이다.

이에 대한 예는 다음과 같다.

(교수님 실수한듯 (18/7 임))

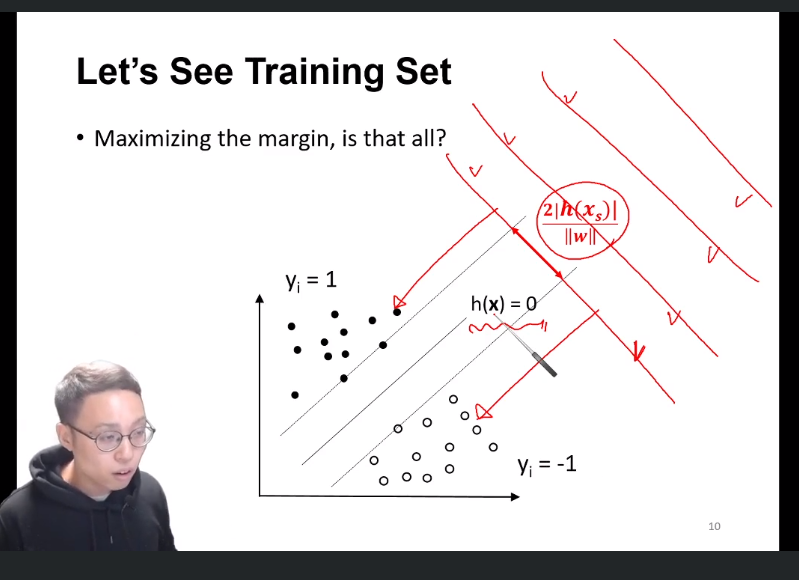
이제 외부의 점 과 h(x)와의 거리를 알았고 margin으로 표현해주면 다음과 같은데, 이 margin을 최대화 해주면 끝나는걸까? -> x

h(x) = 0인 hyperplane이 위 슬라이드처럼 엄청 많이 나올것이고 우리는 그중 classify를 잘 하는 hyperplane이 필요하다.

즉,

h(xi) > 0 when gi = 1

h(xi) <> 0 when gi = -1

이라는 h의 constraint 하에, margin을 maximize 해야한다.

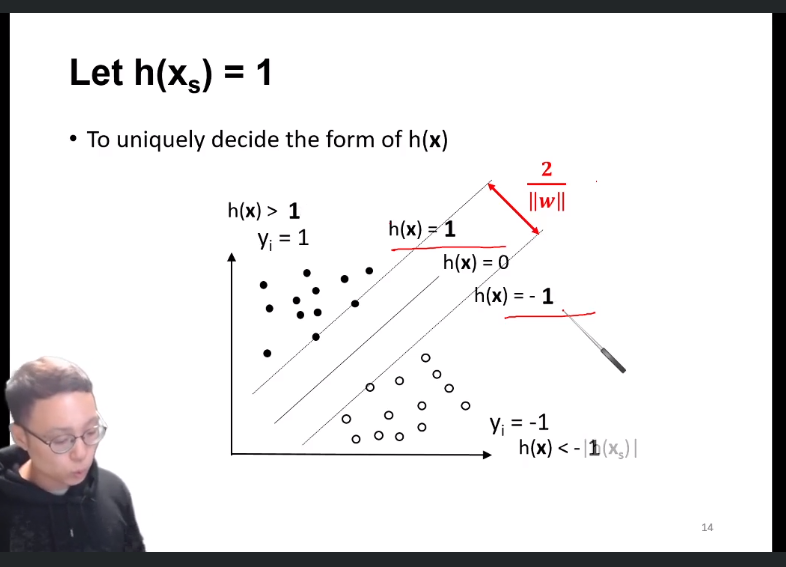
h(xi) > h(x) (=딱 가운데에 있는 hyperplane) 보다 빡센 조건인 h(xi) > h(xs)(xs = upper bound support vector)를 기준으로 하자.

yi = 1일 때, h(xi) > lh(xs)l를

yi = -1일 때, h(xi) < -lh(xs)l를

모든 xi에 대해 만족하는지를 살펴보고, 만족할 경우의 hyperplane만 boundary로 인정한다!

이 조건을 한줄로 표현하면, 다음과 같다.

저 두 부등식에 yi만 곱해주면, 한줄로 표현이 가능하다.

저 한 줄을 constraint로 가질 때, margin을 최대화 시켜주는 h(x)를 찾으면 된다.

이제 constraint, f(x)가 모두 정해졌으니 라그랑쥬 승수법을 쓸 수 있게 되었다.

만약, h(xs)가 1이 되도록 xs 값을 정하면, w도 이에 맞게 fit 될 것이고(이는 결과에 아무런 영향x, 4-0 참고) 식이 매우 간단해질 것이다.

9.2

5. KKT condition과 라그랑쥬 승수법

∇f = λ∇g(auxiliary form 으로 나타낼 시 ∇w,b,mL = 0)
constraint : g(x) <= 0

에 더하여,

mg(x*) = 0
m >= 0

조건을 만족하도록 SVM을 진행할 차례이다.

이 때 수학적 편의성을 위해 f(x), constraint를 다음금과 같은 꼴로 바꾸어준다.

따라서 L(auxiliary function)은 다음과 같다.

우리가 정해야 하는 parameter는, m, w 그리고 b 이다.

∇w,b,mL = 0 그리고 KKT condition을 만족시키는 w, b를 구할 것이다.

L을 w, b, ml에 대해 편미분 했을 때 (0, 0, 0)을 만족하는 점이 llwll/2를 minimize하는 점일 것이다.

5-1 w,b에 대해서 편미분 하기

m = 아직 안정해 졌으므로 variable이다.

w, b에 대해 L을 편미분하여 다음과 같은 ∇w,b = 0으로 만들어주는 optimal한 w, b일 것이다.

그 다음 m로 편미분 하기 전에, KKT condition을 따져보면,

mi >= 0이어야 한다.

조건 1 : m = 0일때에는 constraint가 f(x)에 영향을 미치지 x

조건 2 : m > 0일 경우에는 optimal point x에서 g(x)=0

support vector는, 1 = h(xs)를 만족시키는 점이다.

즉 조건 2 : g(x) = 0 를 만족시키는게 support vector이다.

다시말해

조건 1 :m = 0을 만족시키는 경우는 support vector가 아닌 vector들의 경우이고,

조건 2 : m > 0을 만족시키는 경우는 g(x) = 0인 support vector인 경우이다.

(조건 4개 보기)

∇w,bL = 0 을 이용하여, 즉 w와 b를 이용하여, L을 좀 더 간략한 형태로 만든 모습 이다.

이제 저 L을, m에 대해 편미분하여 =0꼴로 만들어주는 m을 구하면 된다,

이제 optimal한 m을 구했다고 하면, w,b를 알 수 있다.

support vector가 아닌 벡터들 : mi = 0

support vector들 : mi > 0 (mg(x) = 0에서 g(x) = 0)

따라서 g(x) = 0을 통해 b를 구할 수 있다.

만약 support vector가 3개라면, b는 그 값들을 평균내준 값이다.(마지막 줄)

m를 통해 optimal한 w, b를 구했으니, hyperplane을 구했다고 할 수 있다.

이제 구한 이 h(x)를 가지고, classify를 진행할 수 있다.

9-3

6. SVM with kernel trick

6-1. margin

hard margin일수록 outlier에 엄격하고,

soft margin일수록 outlier에 관대하다.

1, 2의 경우엔, 그래도 inlier인 경우이지만 3은 확실히 outlier인 경우이다.

이 떄 크사이를 이용해 어느정도 outlier에 대해 용인해 준다.

그 때, 허용 하더라도 최소화 하는 크사이를 찾는 과정은 다음과 같다. 0<= 크사이 < 1

크사이를 minimize term(object function)에 넣어버리 최소화하는 크사이를 찾을 수 있다.

C는 내가 크사이를 얼마나 허용할 것이냐 의 term이다.

C가 클수록, 크사이가 조금만 커져도 objective function이 커진다.

따라서 outlier에 민감해 진다 라고 볼 수 있다(hard margin)

6-1. kernel trick

optimal한 w, b를 구할 때 term인 L(m)에서, xj^T * xj를 kernel function을 통해 고차원 매피오딘 효과를 낸 식이다.