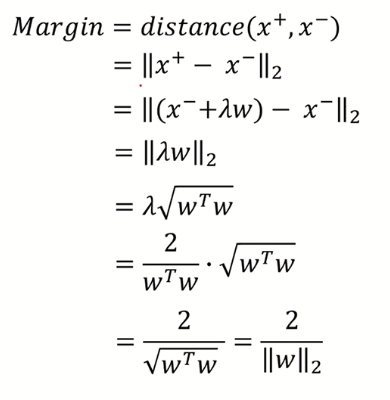SVM(Support Vector Machine)
by
본 포스팅은 여기를 참고하여 만들었습니다.
SVM 이란?
고차원 quadratic programming 방식을 통해 고차원 데이터 분류에 굉장히 좋은 성능을 보인다.
모델은 training data에 대해 성능이 좋아야 하지만, 너무 좋으면 overfitting이 일어나고, test data에 대한 성능은 그에 따라가지 못한다.
Test data 와 train data에 대한 성능에는 trade off 관계가 있는데, train data 에 대한 에러율을 줄이면, test data에 대한 에러율도 줄어듦을 이용한 특성을 이용한 모델이, SVM이다.
SVM은 탄탄한 이론에 근거한(staticical learning theory) 모델이기에, 널리, 그리고 많이 사용된다.
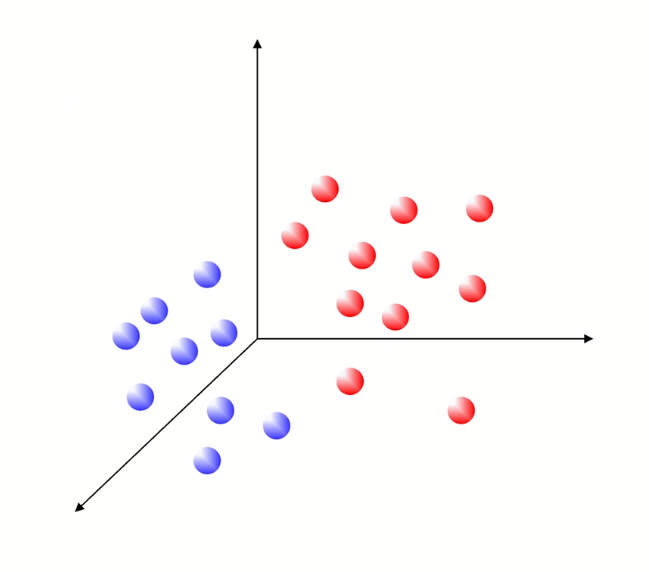
3차원 공간상 class 두 개에 대한 구분선 hyper plane을 찾는 task이다.
구분선은 2차식에서는 선, 3차식에서는 면, 4차식에서부터는 hyperplane이라고 한다.
w는 기울기, b는 bias인 상황에서, 궁극적인 목적은 데이터가 주어졌을때 구하고자하는 w와 b를 찾는 것이다.
클래스를 나눌때 수많은 hyperplane이 있을것인데, 그 중 최적의 hyperplane과 그 hyperplane을 찾는 기준에 대한 방법론이 SVM이다.
이론
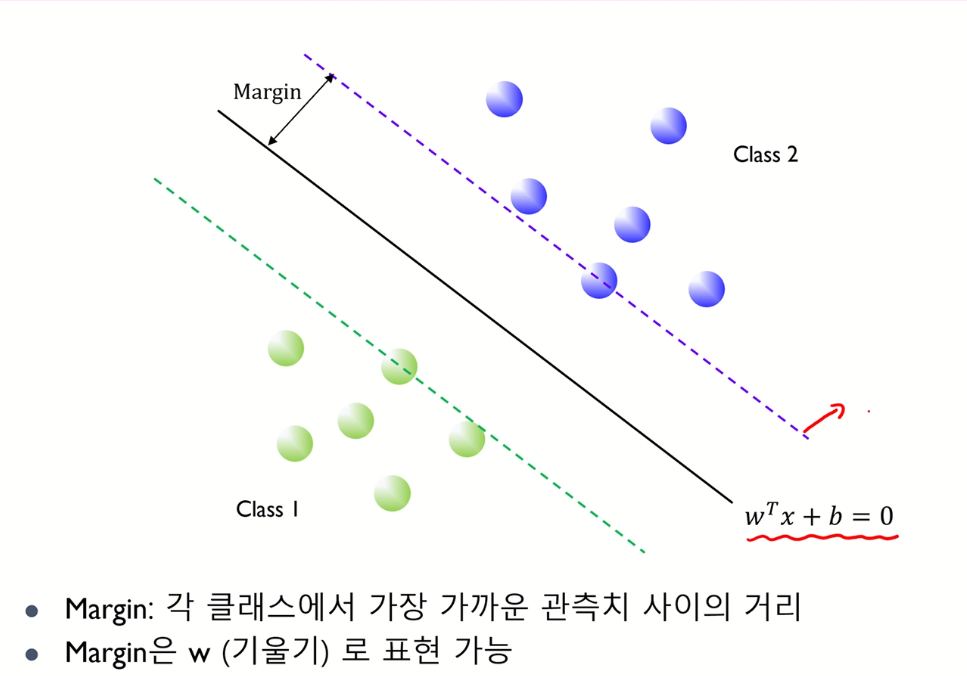
Margin이란 두 class 에 속하는 원소 중 가장 가까운 두 원소 사이 거리를 의미한다.
그림으로 이해하면, 초록색 hyperplane과 보라색 hyperplane 사이 거리이다.(경우에 따라 이 두 거리의 반을 margin이라고 하기도 한다.)
Margin을 최대화 하는 hyperplane(검은 선)을 찾는 것이 SVM의 궁극적인 목적이다.
Margin을 수학적으로 정의해 보면, 보라색 plane을 plus plane이라 하고, 초록색 plane을 minus plane이라 하면, plus plane 은 minus plane 과 상수 만큼 차이나고 이를 이용해 분배법칙으로 식을 다시 나타낼 수 있다.
또한 λ 역시 hyperplane의 기울기인 w에 관한 식으로 나타낼 수 있다.
이 떄 w^t * w를 L2 norm에 관한 식으로 나타낼 수 있다.
이제 margin을 앞서 구한 λ의 w에 관한식, 그리고 w^t * w 을 변환한 식인 w의 L2 Norm을 조합하면, 아래와 같은 식이 나온다.
Margin을 최대화 하려면, 분모에 있는 ||w||2가 작아야한다. (상수인 2는 무시)
이 때 계산상의 편리함을 위해, 제곱근이 껴있는 ||w||2 대신 ||w||2^2를 쓴다.

(subject to 는 제약식의 표현, 원래 뜻 : ..에 달려있다.)
제약식에 따르면, 두 hyperplane 사이 거리인 margin이 최소 1 이상이도록 하는 조건 하에 hyperplane의 기울기 w를 찾는다. (이해 x)
위에서 Decision variable은 찾고 싶은 w와 b
Objective function(목적식)은 최소화 하고싶은 ||w||2^2 (margin의 역수)
Constraint(제약식)은 (2차원상 직선으로써)training data를 완벽히 linear 하게 seperate 해주는 조건이라 할 수 있다.(즉 + 쪽인지 - 쪽인지 확실히 구별 가능하다는 뜻)
목적식이 w2 norm의 제곱인 2차식이므로, quadratic하고, 제약식이 linear(1차식)하므로, 본 경우는 quadratic programming (2차 계획법)이라 한다.
Quadratic programming는 convex optimazation이라 하는데, 2차함수 이기에 최대, 최소 값이 각각 하나만 존재한다.
2차 함수의 최대, 최소값을 찾는 방법을 이용하면, 그 최대, 최소값에서의 w와 b를 찾을 수 있다.

앞서 말한 목적식인 ||w||2^2을 제약식이 적용된 상태에서 최소화 하는 과정에서, Lagrangian multiplier 사용할 수 있다.
Lagrangian multiplier은 두 개의 목적식과 제약식을 하나의 식으로 만들어주는 기법이다.
Lagrangian은 minmax(maxmin) 문제이다.
Primal form을 minimize 시킨 후, dual form을 maximize시킨다.

목적식인 ||w||2^2을 최소로 하는 w와 b를 찾는데, 이 때 극값을 찾는 경우이므로 미분을 이용한다.
w와 b에 대해 각각 한번씩 미분한다.
1 과정에서 1/2 * ||w||2^2을 w에 대해 미분하면 w가 나오고 (w는 (w1, w2, w3)과 같은 1열의 행렬)… w1, w2, w3..wn 에 대해 n 번의 편미분 해주었다고 생각), 마찬가지로 시그마 식을 w에 관해 미분하면 ayx꼴이 나옴을 알 수 있다.
2 과정은 간단하다.
Primal 문제를 1, 2과정을 통애 얻었으니, 목적인 w와 b를 찾아야하는데, 1과정에서 구한 ayx 꼴에서 x,y는 input으로 주어졌지만 a가 주어지지 않았다.
a는 Lagrangina multiplier 과정에서 제한조건 등식 하나마다 더해준 알파값이다.

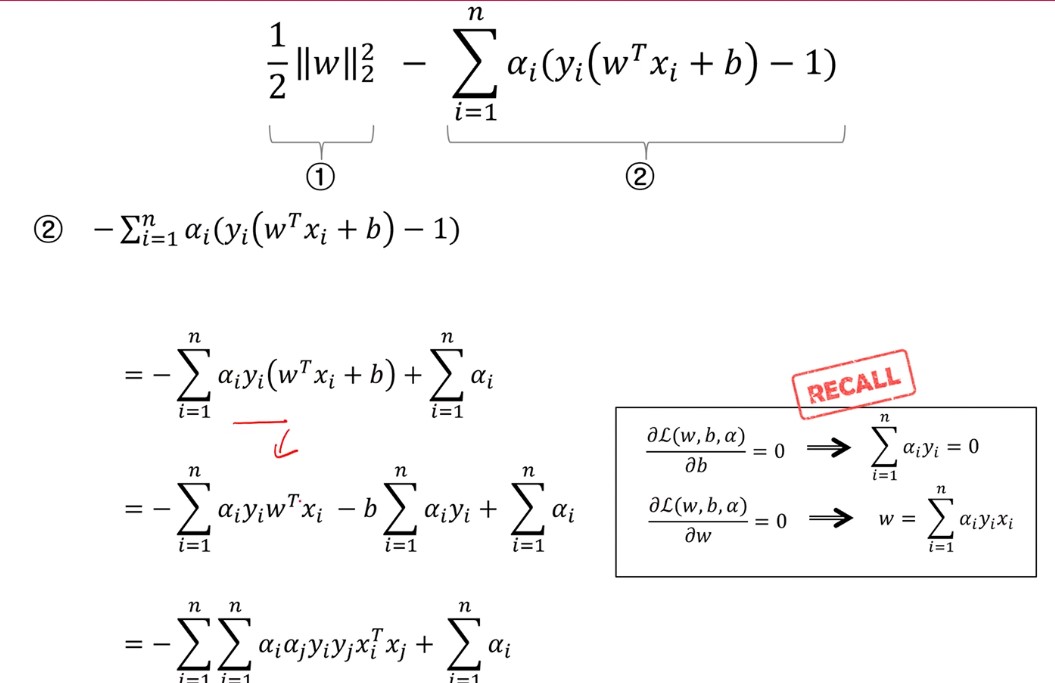
1, 2과정에서 얻은 식을 대입한 모습이다.
위 과정에서 얻은 식을 정리하면, 이와 같은 값이 나온다.
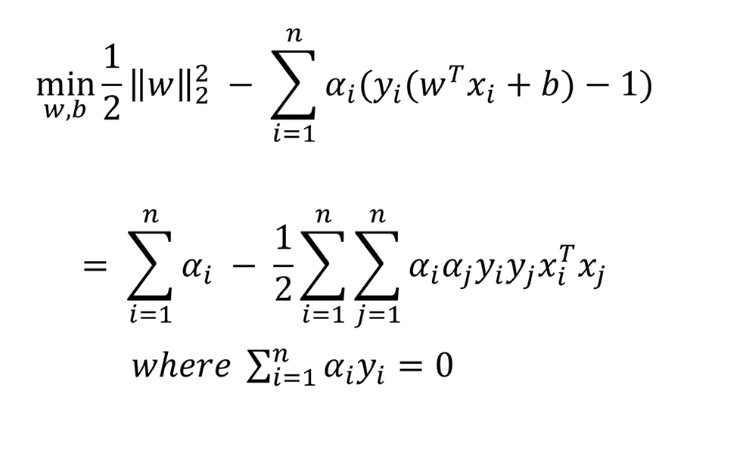

이는 minmax problem이, a 값만 구하면 되는 dual problem으로 바뀐 모습을 보인다.(이해 x)
위 maximize로 시작하는 줄은 목적식 : 식을 최대로 하는 a값 찾기 이고, 아래 subject 부분은 제약식임을 나타낸다.
a 는 궁극적 목표인 w를 구하는데 필요한 과정이다.
KKT(Karush-Kuhn-Tucker) condition

KKT(Karush-Kuhn-Tucker) condition 은 앞서 찾고자했던 a를 구하는 듀얼 문제를 풀기위한 조건이다.
즉 앞서 얻은 Primal solution 그리고 Dual solution의 관계에서 도출된 조건이다.
Stationaly는 앞서 본 미분점 조건, feasibility는 두 solution에서의 제약식, 그리고 complementary slackness는 위 두 제약식 조건을 곱하면 0이 되어야 한다는 조건이다. (이해 x)
아래 사진은 complementary slackness을 만족시키기 위한, 솔루션의 경우의 수이다.
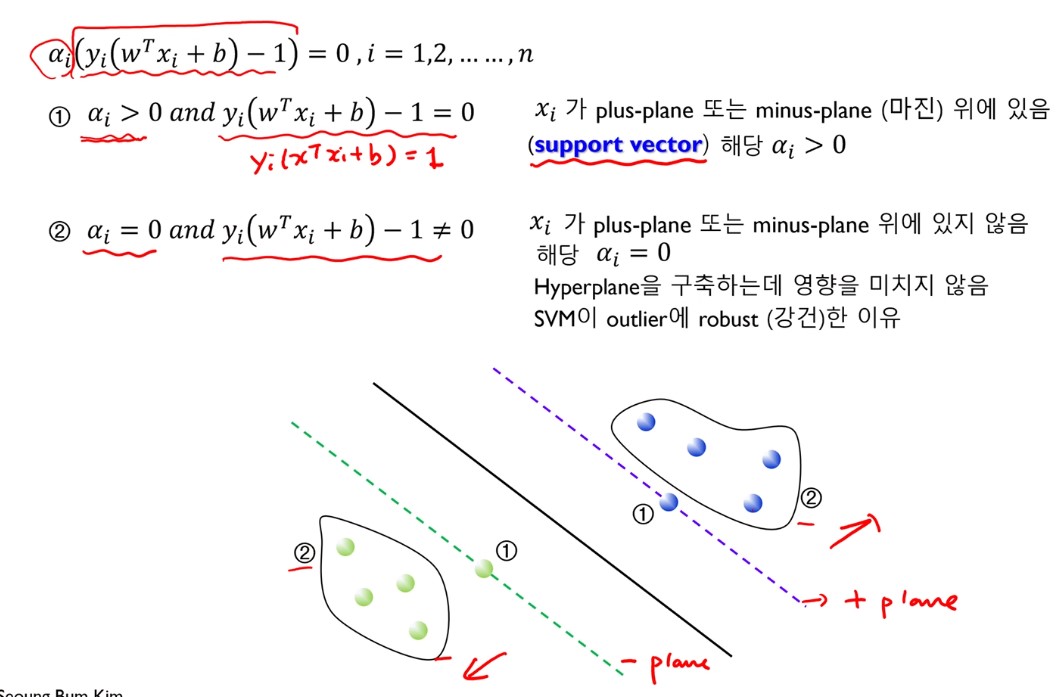
a가 0이 아닌 경우, x가 plus 또는 minus plane 위에 있는 모습을 보여준다.

w는 서포트 벡터인 점들의 합으로 구해지고, 임의의 서포트 벡터 좌표 값을 대입해 b*값을 구할 수 있다.
결국 w와 b를 찾았으므로, SVM모델을 완성했음을 알 수 있다.

반정도밖에 이해 못했다
Hands on ML 으로 공부한 내용
SVM은 분류 과정에서만 사용하는 모델인줄 알았지만, 분류를 포함한 회귀, 이상치탐색에도 아직까지 널리 쓰이는 모델이다.
SVM에서 풀고자 하는 문제는 어떻게 하면 decision boundary를 잘 칠수 있을까? 이다.
Subscribe via RSS