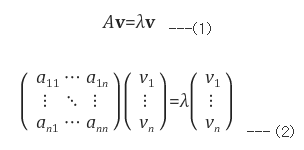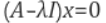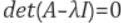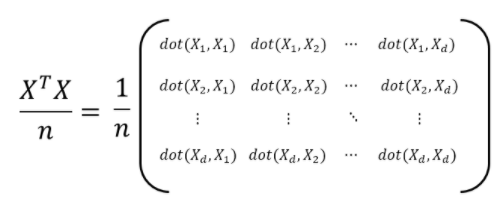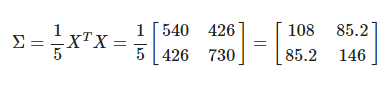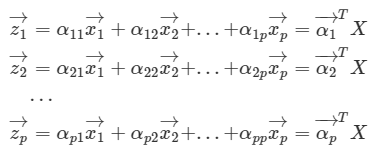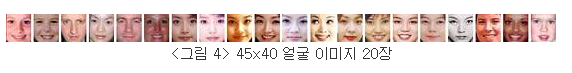[https://darkpgmr.tistory.com/110] (https://darkpgmr.tistory.com/110) 를 참고하여 포스팅한 글입니다.

Eigenvalue and Eigenvector

Eigenvalue and Eigenvector의 의미

선형 변환(superposition을 만족하는 변환, 행렬 곱) A에 의한 결과가, 자기 자신의 상수(lambda) 배가 되는 0이 아닌 벡터를 Eigenvector(고유벡터)라 한다.

그리고 이 때 lamda값을 Eigenvalue(고유값)이라 한다.

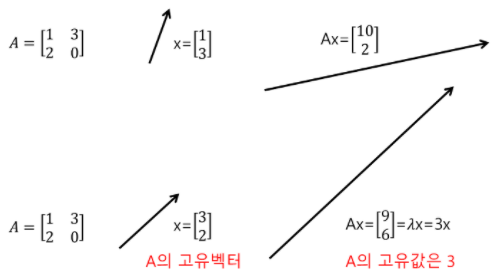
위 그림의 첫 행은 A의 고유벡터를 잘 찾지 못한 경우이고,

두 번째 행은 A의 고유벡터를 x 라고 찾은 후 A를 고유 값인 3이라 나타낸 모습이다.

즉 A 를 고유벡터 x에 곱한 것이, 상수 3을 고유벡터 x에 곱한 것과 동치이다.

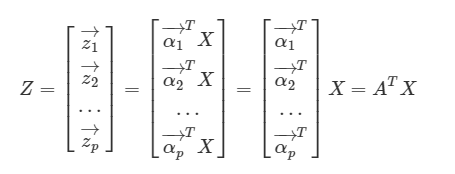
Eigenvalue and Eigenvector 도출

x가 만약 영벡터라면 앞의 항과 상관 없이 좌변의 값이 0이 된다.

따라서 위 term을 만족해야 하고 만족시 lambda 값을 구할 수 있다.

PCA

벡터의 정사영

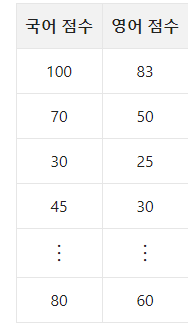
국어 점수와 영어 점수를 종합하여 점수를 얻는 방식을 취한다 할 때, 어떤 반영비로 종합 점수를 얻어야 가장 종합 점수를 잘 나타낼까?

상대적으로 영어 점수가 국어 점수보다 낮으니 국어 : 영어 반영비를 약 3:2로 하면 이상적인 종합 점수를 얻을 수 있을 것이다.

여기서 이 “반영비” 를 벡터라 생각 하자.

그리고 이 벡터에 내 국어,영어 점수(70, 50)를 내적(정사영)을 취해주면, 종합 점수가 나올 것이다.

PCA란, 데이터를 어떤 벡터(반영비)에 내적해야 최적의 결과를 나타내어 줄까? 에 중점을 둔 개념이다.

이 최적의 벡터(반영비)를 찾는 방법은, 공분산 행렬이다.

공분산 행렬

공분산 행렬은 각 특징 쌍(각 row라 생각)이 얼마나 닮았는지를 보여주는 행렬이다.

고유벡터, 고유값과 공분산 행렬

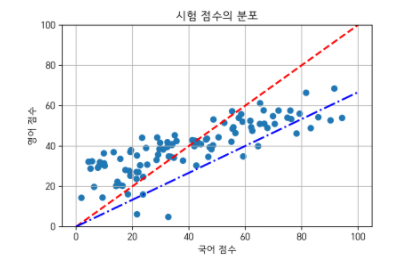
고유벡터는, 그 행렬(분포, A)이 벡터에 작용하는 principle axis(주축)의 방향을 나타낸다.

즉 그 분포를 가장 잘 나타내는 벡터를 의미한다

위 문장은, 데이터를 고유벡터와 비교해 보니, 고유벡터가 데이터를 잘 긋더라.. 하면서 얻은 결론이라 생각한다.

(고유벡터는 어떠한 선형 벡터 A를 고유벡터에 행렬곱한 결과와, 상수 lambda를 벡터 A에 곱해준 결과와 같을 때의 이 벡터를 의미한다.)

(위 그림에서 파란색 선을 고유 벡터라 생각.)

고유 값은 고유 벡터 방향으로 얼마만큼 벡터공간을 늘려줄지를 의미한다.

따라서 고유값이 큰 순서대로 고유 벡터를 정렬하면 결과적으로 중요한 순서대로 주성분을 구하는 것이 된다고 한다.

데이터 벡터를 어떤 벡터에 정사영(내적) 하는 것은, 최적의 종합점수를 표현해 주고 이 정사영은 공분산행렬의 고윳값과 고유 벡터를 구함으로써 가능하다.

공분산 행렬의 수식적 유도 및 의미

https://angeloyeo.github.io/2019/07/27/PCA.html

여기에 자세히 나와있다.

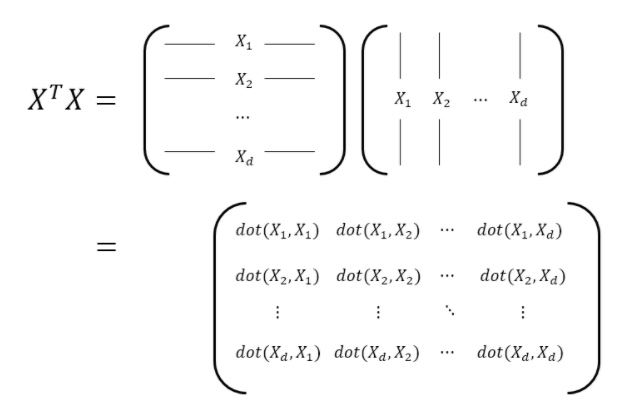
각 열의 평균이 0인 공분산 행렬을 X라 할 때,

(X^T)X 의 i행 j열의 성분은, 행렬 X의 i번째 feature(열)과 j번째 열이 얼마나 닮았는지를 알려준다.

공분산 행렬은 데이터 샘플수 만큼 그 크기를 앞에서 나누어주어 다음과 같이 일반화 할 수 있고,

실제 예시는 다음과 같다.

(1,2), (2,1) 성분이 나타내는 바는, X의 1번째 feature(열)의 변화가 2번째 feature의 변화와 85.2의 수치만큼 연관이 있다(닮았다)를 나타낸다.

PCA의 목적

PCA의 목적은 행렬(분포)의 분산을 최대한 보존하는데에 있다.

다시말해 원데이터 X의 분산을 최대한 보존해야하고, 따라서 Z의 분산 역시 최대화 되어야 한다.

고유벡터에 정사영 되었을 떄 최대 variance

여기서 시그마는 공분산 행렬을 뜻하고,

라그랑주 승수법에 의해 eigenvector를 통해 정사영 했을 때 variance는 eigenvalue 이다.

PCA와 얼굴 인식

https://darkpgmr.tistory.com/110 에 자세히 나와있습니다.

이미지에서 픽셀 밝기값을 일렬로 연결하여 45x40 = 1800차원의 벡터로 얼굴 이미지를 생각한다.(1800차원 공간상의 한점의 좌표에 대응)

1800차원의 데이터를 PCA를 수행하면 1800차원의 주성분 벡터를 얻을 수 있다.

이렇게 얻어진 주성분 벡터를 이미지로 다시 plot 한 것이 eigenface이고, 분산이 큰 순서대로 처음 20개를 나열하면 다음과 같다.

위 그림들을 보면, eigenfaces들은 데이터의 공통된 요소(전반적인 얼굴 형)을 나타내고, 뒤로 갈수록 세부적인 차이 정보를 나타낸다.

PCA를 통해 얻어진 주성분 벡터들은 서로 수직인 관계를 갖는다.

이 말은 주성분 벡터들은 n차원 공간을 이루는 기저라는 말이다.

즉, PCA로 얻은 주성분 벡터들을 e1, e2, …, en라면 임의의 n차원 데이터 x는 x = c1e1 + c2e2 + … + cnen과 같이 ei들의 일차결합으로 표현될 수 있다.

이 떄 상수계수 ci는 x 와 ei의 내적으로 즉 ci = x ‘ ei 으로 나타낼 수 있다. (i가 1에 가까울 수록 클 것이라 생각됨. 1번째 주축이 분포와 가장 많이 닮았으므로)

i가 숫자가 커질수록, 즉 뒷부분의 주성분 벡터들은 데이터 분포에 포함된 노이즈성 정보를 나타낸다.

따라서 뒷부분은 버리고 전반부 k개의 주성분 벡터들만을 가지고 원래의 데이터를 표현

(원래의 x가 x = c1e1 + c2e2 + … + cnen일 때 xk = c1e1 + … +ckek로 x를 근사)

하면, 노이즈가 제거된 데이터를 얻을 수 있다.