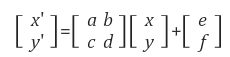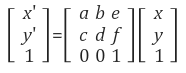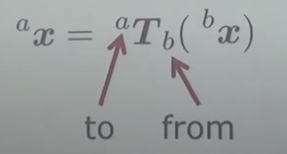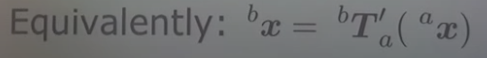https://www.youtube.com/watch?v=Qn9enAA5j38&t=495s에서 강의를 보실 수 있습니다.

https://darkpgmr.tistory.com/79를 참고하여 작성한 포스트입니다.

Geometric transformation

기하학적 변환을 뜻한다.

본 강의에선 image 간의 shift, scale등의 변형을 주제로 다룬다.

카메라 관점에서 projection한 이미지는 왜곡되기 마련이다.

이를 원래대로 매핑하여, distorted 된 non rectified 이미지를 rectify 하거나,

반대로 rectified 된 이미지를 다른 3D와 같은 부분에 와핑하여 텍스쳐와 같은 질감을 더하려

와핑해 주는 것 역시 geometric transform에 포함된다.

Affine transformation

Affine 변환은 직선, 길이의 비, 평행성, 즉 쉽게말해 기하학적 성질을 보존해주는 변환이다.

Affine 변환을 거친 후에도 평행한 선들은 평행한 상태로 유지된다.

이 변환은 주로 이상적이지 않은 카메라 각도에서 발생하는 기하학적 왜곡이나 형태 변형을 보정하는데 주로 쓰인다.

Affine 변환의 일반식, Homogeneous 식이다.

Homogeneous 식은 회전, 스케일링, 평행이동이 행렬 변환 하나로 표현된 식이라 볼 수 있다.

210513 추가 내용

2차원 벡터, 점에 본 행렬을 곱하여 벡터,점의 회전, 이동등을 보려할 때,

벡터는 위치를 표현 하지 않고 크기와 방향만 표현, 즉 V = [x, y, 0]^T

점은 위치만 표현함을 고려할 때 ,

점을 회전, scaling, 이동을 표현하기 위해 V = [x, y, 1]^T 로 표현한다.

즉 벡터와 점의 affine transform을 한 번에 보기 위해선 각각 colomn matrix에 0, 1을 추가하여 transform해주고, 이를 homogeneous system이라 한다.

본 식은 b의 coordinate에서 a의 coordinate로 transform 했음을 의미한다.

a 의 coordinate에서 b의 coordinate로 transform 하는 역변환 역시 가능함(만약 T가 invertible 하다면)을 볼 수 있다.

Resampling

내 transform이 그 값을 정수가 아닌 값으로 lead 할 경우, resampling 작업이 필요하다.

픽셀을 옮기는 과정에서 소수 단위의 위치가 무시되어 정확한 위치 변환이 이루어 지지 않기 때문이다.

강의에서 배운 interpolation 기법들에 대해 설명해 보겠다.

Nearest neighbor interpolation

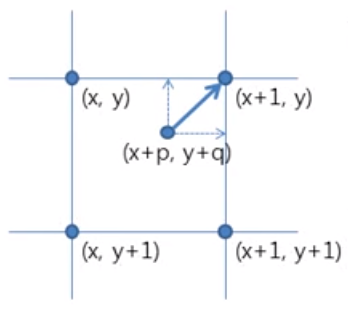
그리드 상의 점 중 가장 가까운 값으로 선택하는 방법이다.

x+p. y+q를 반올림 하여 해당 위치의 픽셀 값을 가져온다.

Bilinear interpolation

값을 구하려는 픽셀 주변의 픽셀 값 4개의 변화 양상을 추정하여 픽셀 값을 구하는 것이다.

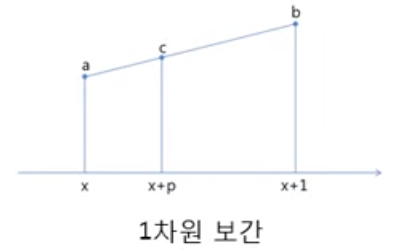
x를 0이라 할 때, a-b 직선 함수는 y=(b-a)x + a 로 나타낼 수 있다.

그리고 p(x= 0이기에 x+p를 대입한 것과 동일)를 대입해 보면 c는 (b-a)p + a가 된다.

이를 정리하면 c는 (1-p)a + pb로 나타낼 수 있다.

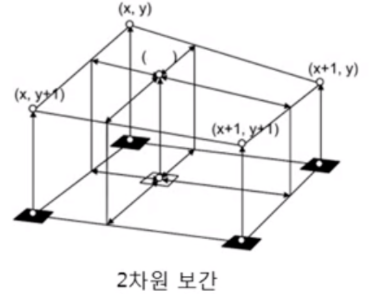
이를 2차원으로 나타낸 것이 bilinear interpolation 이다.

1차 보간을 두 번 수행 한 것이다.

의 결과를 갖는다.

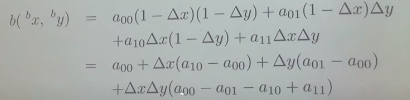
Bicubic interpolation

선형(bilinear) 보간법이 1차함수를 사용했다면, bicubic interpolation은 3차 함수를 사용한다.

3차함수를 사용하면 1차함수를 사용하는 것 보다 훨씬 더 부드러운 결과를 만들 수 있다고 한다.

https://bskyvision.com/789 여기 보고 공부하기

의 결과를 갖는다.

bicubic interpolation은 총 16개의 점을 참조함으로, 더욱 더 정교하에 interpolate 함을 알 수 있다.

세 interpolation 기법을 비교하자면,

speed : NN » Bilinear » Bicubic

성능 : NN « Bilinear «  Bicubic

으로 볼 수 있다.

forward and inverse warping

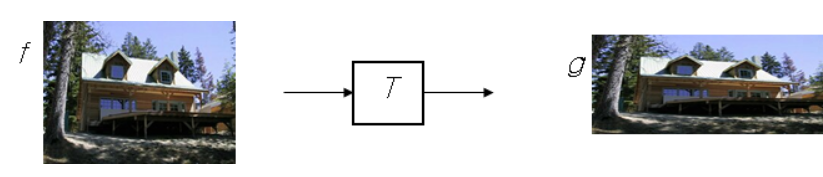
forward warping

https://m.blog.naver.com/pine-93/221414007061 참고하기

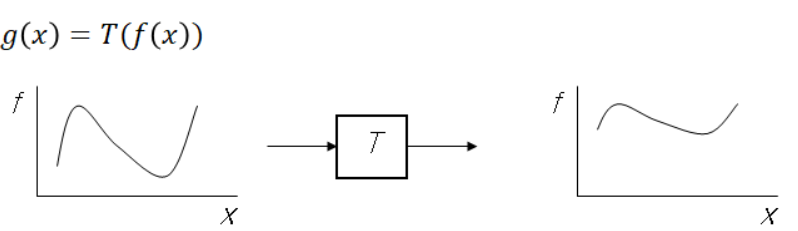
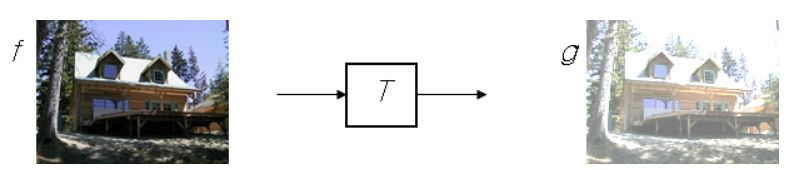
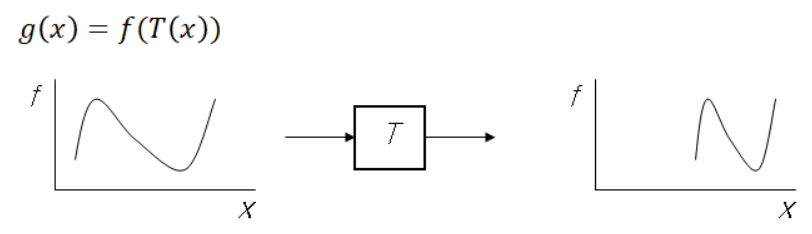
이미지의 픽셀의 intensirt 값을 바꾸는 filtering과 달리, warping은 좌표 값을 바꾸는 것이다.

Filtering은 그림을 보면 알 수있듯, x의 좌표값은 그대로이지만 intensity 값은 바뀌었다.

반대로 warping은 그래프의 모양은 그대로지만 x의 범위가 바뀌었다.

이 warping은 Affine transform에서 살펴본 matrix들을 통해 가능하다.

forward warping 을 진행하면 integer pixel location value가 non-integer pixel location valud로 매핑되어 interpolation이 필요하다.

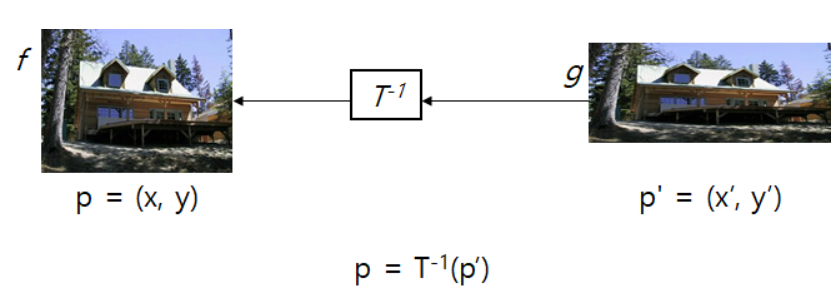
Inverse warping

앞서 말했듯이 forward warping을 진행하면 non-integer로 매핑되기에 output image에 missing pixel이 발생한다.

Inverse warping을 통해, 이러한 문제를 해결 가능하다.

Inverse warping은 원본 영상에 존재하지 않는 위치를 결과 영상에 할당하는 과정인데, 다음과 같은 transformation을 통해 p를 계산한다.

쉽게 말해 forward warping은 upsampling 하기에 output image에 hole이 발생하고, inverse warping을 사용하면 downsampling 이기에 해상도 저하가 발생한다.

이 부분도 interpolation으로 해결한다.