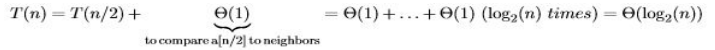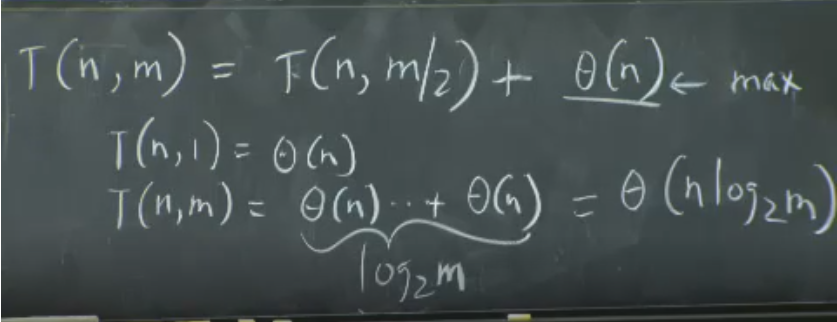본 강의는 여기에서 들으실 수 있습니다.

총 24강으로 이루어져 있습니다.

1강

(좌측,우측 단은 옆 1개 원소보다만 크면 됨)

이 배열을 A, 원소 갯수를 n이라고 하자. 기존 내 방법은 큰 틀로

for i in range(n):
        if ((A[i] > A[i-1])) and (A[i] > A[i+1])): #예외처리는 생략
        break
print(A[i])

와 같은 방식으로 접근했을 것이다.

더 효율적인 방법으로, 이진트리 방법이 있다.

n/2이 되는 점을 기준으로 잡고, 그 지점에서 트리를 지정해서 뻗어간다.

while True:
    if (A[n/2]<(A[n/2]+1):
        
    elif (A[n/2]<(A[n/2]-1):

    else :
    #(A[n/2]이 극대값

과 같은 방식으로 접근하면 효율적 접근이 가능하다.

그림은 다음과 같다.

(극소값의 경우)

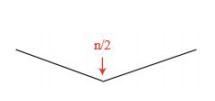
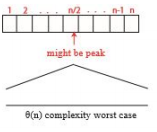
크기가 n인 입력을 받았을때 알고리즘의 실행시간을 T(n)이라 한다.

worst case complexity는 O(n)이라 한다.(그냥 Time complexity 나타내주는 척도로 생각)

그리고 이진트리를 사용한 T(n)은,

T(1) + T(1) + T(1) + ...
=O(1) + O(1) + O(1) + ...
=O(log(n)) 이다.  이다.  (로그의 밑은 2)

n이 1000만이면, O(n)은 13 초가 걸리는데에 반해, O(log(n))는 0.001초가 걸린다.

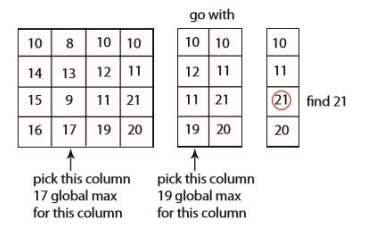
2차원 배열에서로 확장해 극대값을 찾아보자면,

복잡도 비교

(1차원)

(2차원)